“Finite Field Arithmetic.” Chapter 7: “Turbo Egyptians.”
This article is part of a series of hands-on tutorials introducing FFA, or the Finite Field Arithmetic library. FFA differs from the typical "Open Sores" abomination, in that -- rather than trusting the author blindly with their lives -- prospective users are expected to read and fully understand every single line. In exactly the same manner that you would understand and pack your own parachute. The reader will assemble and test a working FFA with his own hands, and at the same time grasp the purpose of each moving part therein.
- Chapter 1: Genesis.
- Chapter 2: Logical and Bitwise Operations.
- Chapter 3: Shifts.
- Chapter 4: Interlude: FFACalc.
- Chapter 5: "Egyptological" Multiplication and Division.
- Chapter 6: "Geological" RSA.
- Chapter 7: "Turbo Egyptians."
You will need:
- All of the materials from Chapters 1 - 6.
ffa_ch7_turbo_egyptians.vpatch(see here)ffa_ch7_turbo_egyptians.vpatch.asciilifeform.sig- ffa_ch7_turbo_egyptians.kv.vpatch
- ffa_ch7_turbo_egyptians.kv.vpatch.asciilifeform.sig
Add the above vpatch and seal to your V-set, and press to ffa_ch7_turbo_egyptians.kv.vpatch.
You should end up with the same directory structure as previously.
Now compile ffacalc:
cd ffacalc gprbuild |
But do not run it quite yet.
No one submitted a solution to the "trivial optimizations" problem posed in Chapter 5, but reader Diana Coman did show symptoms of knowing the magic ingredient which happens to be the subject of this Chapter.
The attentive reader may already have begun to suspect that the "Egyptian" multiplication algorithm (FZ_Mul_Egyptian from Ch. 5) is not the final word on the subject of integer multiplication in FFA. But before we can explore subquadratic multiplication (and -- much later -- clever methods for speeding up modular reduction) it is necessary to set up the arena for a "fair fight", by making reasonably well-optimized variants of both of the quadratic-runtime "Egyptian" algos, FZ_Mul_Egyptian and FZ_Mod.
Previously, the primary design objectives of the FFA algorithms were correctness and constant-spacetime operation; followed, secondarily, by simplicity (in the fits-in-head sense.) In this chapter, we add another objective: speed.
At no point will correctness or constant-spacetime (branch-free and offsetting-by-secrets-free) operation be sacrificed under any pretext whatsoever. However, in order to obtain, e.g., an RSAtron that is practically usable on commonplace machines, it will be necessary to sacrifice a certain amount of mechanical simplicity. This Chapter, along with the bulk of the remaining material, will be devoted to this painful -- but not uninteresting! -- task.
Let's begin with a new, "turbo" FZ_Mul_Egyptian:
FZ_Mul.adb:
-- 'Egyptological' multiplier. XY_Lo and XY_Hi hold result of X*Y. procedure FZ_Mul_Egyptian(X : in FZ; Y : in FZ; XY_Lo : out FZ; XY_Hi : out FZ) is L : constant Indices := X'Length; -- Register holding running product XY : FZ(1 .. X'Length + Y'Length); -- X-Slide XS : FZ(1 .. X'Length + Y'Length); begin -- Product register begins empty FZ_Clear(XY); -- X-Slide initially equals X: XS(1 .. X'Length) := X; XS(X'Length + 1 .. XS'Last) := (others => 0); -- For each word of Y: for i in Y'Range loop declare -- Current word of Y W : Word := Y(i); -- Current cut of XY and XS. Stay ahead by a word to handle carry. Cut : constant Indices := L + i; XYc : FZ renames XY(1 .. Cut); XSc : FZ renames XS(1 .. Cut); begin for b in 1 .. Bitness loop -- If current Y bit is 1, X-Slide Cut is added into XY Cut FZ_Add_Gated(X => XYc, Y => XSc, Sum => XYc, Gate => W and 1); -- Crank the next bit of Y into the bottom position of W W := Shift_Right(W, 1); -- X-Slide := X-Slide * 2 FZ_ShiftLeft(XSc, XSc, 1); end loop; end; end loop; -- Write out the Product's lower and upper FZs: XY_Lo := XY(1 .. XY_Lo'Length); XY_Hi := XY(XY_Lo'Length + 1 .. XY'Last); end FZ_Mul_Egyptian; pragma Inline_Always(FZ_Mul_Egyptian); |
Observe that the Y-Slide from Chapter 5's multiplier is gone. Instead, we now walk through the bits of the multiplicand Y without having to shift the entire thing FZ_Bitness(Y) times: each word of Y is loaded into W, starting with the first; and the "egyptology" is then performed Bitness times, once for each bit of W.
The other optimization is the introduction of the cut concept. Observe that an addition of two FZ integers of identical bitness, can produce a result with an intrinsic bitness that is larger than that of the greater parent's by a maximum of one bit. The consequence of this is that the Chapter 5 FZ_Mul_Egyptian wastes roughly half of its CPU time shifting and adding words that never, at the particular times they are touched, depart from zero.
Thus, the first iteration of the loop is carried out on a cut of length X'Length + 1; the second, X'Length + 2; and forth; the last iteration is the only one which is performed on the entire XY product-accumulator and the entire XS X-Slide. We "run ahead" of the segment of XY which has been touched, by one word, so as to have a place to which to ripple the carry.
At the expense of a certain amount of "obviousness", we win a 2x gain in multiplication speed.
And now we will apply exactly the same optimizations to the modulus routine:
FZ_Divis.adb:
-- Modulus. Permits the asymmetric Dividend and Divisor in FZ_Mod_Exp. procedure FZ_Mod(Dividend : in FZ; Divisor : in FZ; Remainder : out FZ) is -- Length of Divisor and Remainder; < = Dividend'Length L : constant Indices := Divisor'Length; -- Remainder register, starts as zero R : FZ(1 .. L) := (others => 0); -- Indices into the words of Dividend subtype Dividend_Index is Word_Index range Dividend'Range; -- Permissible 'cuts' for the Slice operation subtype Divisor_Cuts is Word_Index range 2 .. Divisor'Length; -- Performs Restoring Division on a given segment of Dividend:Divisor procedure Slice(Index : Dividend_Index; Cut : Divisor_Cuts) is begin declare -- Borrow, from comparator C : WBool; -- Left-Shift Overflow LsO : WBool; -- Current cut of Remainder register Rs : FZ renames R(1 .. Cut); -- Current cut of Divisor Ds : FZ renames Divisor(1 .. Cut); -- Current word of Dividend, starting from the highest W : Word := Dividend(Dividend'Last + 1 - Index); begin -- For each bit in the current Dividend word: for b in 1 .. Bitness loop -- Send top bit of current Dividend word to the bottom of W W := Rotate_Left(W, 1); -- Advance Rs, shifting in the current Dividend bit FZ_ShiftLeft_O_I(N => Rs, ShiftedN => Rs, Count => 1, OF_In => W and 1, Overflow => LsO); -- Subtract Divisor-Cut from R-Cut; Underflow goes into C FZ_Sub(X => Rs, Y => Ds, Difference => Rs, Underflow => C); -- If C=1, subtraction underflowed, and we must undo it: FZ_Add_Gated(X => Rs, Y => Ds, Sum => Rs, Gate => C and W_Not(LsO)); end loop; end; end Slice; begin -- Process bottom half of dividend: for i in 1 .. L - 1 loop Slice(i, i + 1); -- stay ahead by a word to handle carry end loop; -- Process top half of dividend for i in L .. Dividend'Length loop Slice(i, L); end loop; -- Output the Remainder. Remainder := R; end FZ_Mod; pragma Inline_Always(FZ_Mod); |
In addition to the two optimizations analogous to those we had applied to FZ_Mul_Egyptian, we also get the ability to apply FZ_Mod to a Dividend which exceeds the bitness of the Divisor. This will allow us to abolish the zero-padding of Modulus in Chapter 6's FZ_Mod_Mul.
Correspondingly, we carefully alter the preconditions of FZ_Mod:
FZ_Divis.ads:
-- Modulus. Permits the asymmetric Dividend and Divisor in FZ_Mod_Exp. procedure FZ_Mod(Dividend : in FZ; Divisor : in FZ; Remainder : out FZ); pragma Precondition(Dividend'Length >= Divisor'Length and Divisor'Length = Remainder'Length); |
The only place in FFA where the asymmetric invocation of FZ_Mod will be permitted, is FZ_Mod_Mul, the modular multiplier procedure, which will now look like this:
FZ_ModEx.adb:
-- Modular Multiply: Product := X*Y mod Modulus procedure FZ_Mod_Mul(X : in FZ; Y : in FZ; Modulus : in FZ; Product : out FZ) is -- The wordness of all three operands is equal: L : constant Indices := X'Length; -- Double-width register for multiplication and modulus operations XY : FZ(1 .. L * 2); -- To refer to the lower and upper halves of the working register: XY_Lo : FZ renames XY(1 .. L); XY_Hi : FZ renames XY(L + 1 .. XY'Last); begin -- XY_Lo:XY_Hi := X * Y FZ_Mul_Egyptian(X, Y, XY_Lo, XY_Hi); -- Product := XY mod M FZ_Mod(XY, Modulus, Product); end FZ_Mod_Mul; pragma Inline_Always(FZ_Mod_Mul); |
And now, on the same machine as in Ch.6 , timed and plotted logarithmically:
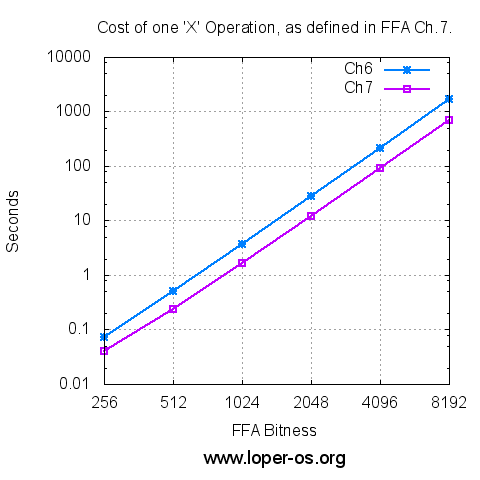
Or, for those who prefer the raw numbers,
| FFA Bitness | Ch.6 'X' (sec) | Ch.7 'X' (sec) |
|---|---|---|
| 256 | 0.072 | 0.040 |
| 512 | 0.505 | 0.240 |
| 1024 | 3.685 | 1.672 |
| 2048 | 27.975 | 12.024 |
| 4096 | 217.966 | 90.439 |
| 8192 | 1720.127 | 699.979 |
And finally, let's turn this into a FFACalc tape, and verify the signature of the Chapter 7 material, using itself, just like we did in the previous chapter:
( the seal of ffa_ch7_turbo_egyptians.vpatch : ) . 88A0984C5438EFD811BA8505362EEA572B4057C52662DA8854DF66613C40332EB8F4E3 80932DBF9106F3536643BD2FF69DA90EA0402B4FDC21A9245C3EBCB10C86C1847C9CC9 9C2ECE4245735013D0E59EE905479445B625D76EECC1BDEEBF489DC512715324995D13 EAB27D286EFA86BF8D69C3D93CB65E2F4BA9B805AA392B29D9F6635E9C7D81C0CC4EAA A2DA0F618D83F7DAB4854F24B3A900BFDF35E58E87745A6A8D11868C860334DD80A4A4 D0DCAC4E5EC34E9C16BBD174659008145F1E09556009557277A7DFE74FAA3018995746 8CB25E0B10B5AE8D114E4E89E4B940B1A21A5BB7EFDD75AB59A1D82AC08DBCC9A7B10F 5B708B2BC2453AB9BC6C80 ( my public rsa exponent : ) . 10001 ( my public rsa modulus : ) . CDD49A674BAF76D3B73E25BC6DF66EF3ABEDDCA461D3CCB6416793E3437C7806562694 73C2212D5FD5EED17AA067FEC001D8E76EC901EDEDF960304F891BD3CAD7F9A335D1A2 EC37EABEFF3FBE6D3C726DC68E599EBFE5456EF19813398CD7D548D746A30AA47D4293 968BFBAFCBF65A90DFFC87816FEE2A01E1DC699F4DDABB84965514C0D909D54FDA7062 A2037B50B771C153D5429BA4BA335EAB840F9551E9CD9DF8BB4A6DC3ED1318FF3969F7 B99D9FB90CAB968813F8AD4F9A069C9639A74D70A659C69C29692567CE863B88E191CC 9535B91B417D0AF14BE09C78B53AF9C5F494BCF2C60349FFA93C81E817AC682F0055A6 07BB56D6A281C1A04CEFE1 ( now modularly-exponentiate it : ) X ( ... and print the output .) # |
... and play the tape! :
$ time cat ch7_rsa_tape.txt | ./bin/ffa_calc 2048 32 |
... and unsurprisingly:
0001FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF003051 300D060960864801650304020305000440FCFB42B5342D226261DF36158BB4EA5482F4 B45B8D4259F3873D8B77CD7572D55FBADCBCC1267BECE169F330154F7A9156C60A07FA 8C902BEE43FB27FC33B248 real 0m12.018s user 0m12.004s sys 0m0.002s |
Guess what? The correct answer. (Use the patched GPG from Ch. 6, and compare.)
Homework:
1. Prove that the new FZ_Mod produces, for all valid inputs, the equivalent answer to the one in the previous chapter.
2. Formulate a hypothesis regarding why the observed speedup of 'X' was greater than two-fold.
~To be continued!~



I just noticed that a trivial optimization is missing:
XYc : FZ renames XY(1 .. Cut); XSc : FZ renames XS(1 .. Cut);of course should have been
XYc : FZ renames XY(i .. Cut); XSc : FZ renames XS(i .. Cut);Quick timings, in seconds:
I ape-ologize for not having noticed this earlier.
Dear apeloyee,
Interestingly, this appears to work; though I am still racking my brains to show in the general case why.
Yours,
-S
Dear apeloyee,
Ok, it in fact makes sense. XYc and XSc "slide in unison".
It is unfortunate that FZ_Mul_Egyptian disappears in Ch. 9; because this is a pretty great trick.
Apeloyee: are your timings for the version given in your comment? or for the classical ones ? it is impossible to compare, lacking both, given as I do not have your iron here.
Yours,
-S
> Apeloyee: are your timings for the version given in your comment? or for the classical ones ? it is impossible to compare, lacking both,
There are both; Ch.7 is the classical, Ch.7-mod is the version given.
Dear apeloyee,
Makes sense, thanks.
Yours,
-S
In the FZ_Divis.adb , in the procedure Slice, why do you have a declare block inside the procedure encompassing the whole procedure? Why not do all that declaration as part of the procedure declaration and move the code up one level (get rid of the declare/begin/end lines)?
Dear PeterL,
Entirely good point, it is redundant. I'll snip it in Ch. 19 and link to your comment.
Thanks,
-S
Dear PeterL,
This item has been included in Ch. 19!
Yours,
-S