“Finite Field Arithmetic.” Chapter 12A: Karatsuba Redux. (Part 1 of 2)
This article is part of a series of hands-on tutorials introducing FFA, or the Finite Field Arithmetic library. FFA differs from the typical "Open Sores" abomination, in that -- rather than trusting the author blindly with their lives -- prospective users are expected to read and fully understand every single line. In exactly the same manner that you would understand and pack your own parachute. The reader will assemble and test a working FFA with his own hands, and at the same time grasp the purpose of each moving part therein.
- Chapter 1: Genesis.
- Chapter 2: Logical and Bitwise Operations.
- Chapter 3: Shifts.
- Chapter 4: Interlude: FFACalc.
- Chapter 5: "Egyptological" Multiplication and Division.
- Chapter 6: "Geological" RSA.
- Chapter 7: "Turbo Egyptians."
- Chapter 8: Interlude: Randomism.
- Chapter 9: "Exodus from Egypt" with Comba's Algorithm.
- Chapter 10: Introducing Karatsuba's Multiplication.
- Chapter 11: Tuning and Unified API.
- Chapter 12A: Karatsuba Redux. (Part 1 of 2)
You will need:
- A Keccak-based VTron (for this and all subsequent chapters.)
- All of the materials from Chapters 1 - 11. (They have been re-ground for the new VTron format; please re-download here.)
- There is no vpatch in Chapter 12A.
On account of the substantial heft of this chapter, I have cut it into two parts, 12A and 12B; you are presently reading 12A, which consists strictly of the benchmarks and detailed analysis of the Karatsuba method presented earlier. 12B will appear here in the course of the next several days, preceding Ch. 13.
First things first:
As noted earlier in Chapter 11:
- Reader apeloyee observed that the modular exponentiation operation is a poor benchmark for multiplication speed, on account of the fact that the current algorithm spends the vast majority of its CPU time inside the Knuth division routine.
- Reader ave1 carefully analyzed the executables generated by AdaCore's x86-64 GNAT, and showed that this compiler is prone to ignore Inline pragmas unless they are specified in a particular way.
- ave1 also produced a fully-self-building, retargetable, fully-static, and glibc-free GNAT.
And so I have carried out a benchmark battery strictly on Multiplication -- naturally, on the standard test machine used for all previous benchmarks -- across a meaningful range of FFA bitnesses (i.e. integers large enough not to fall through the resolution of the timer), across all of the multiplier routine variants offered in chapters 9 - 11:
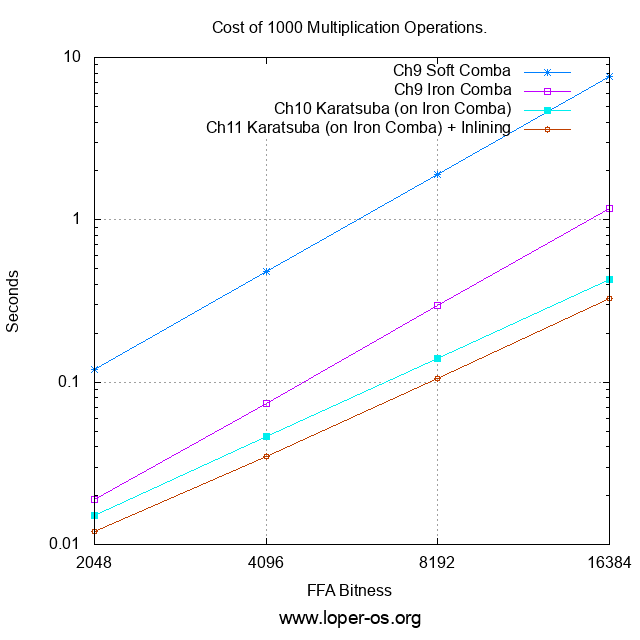
Or, for those who prefer the raw numbers to the logarithmic plot,
| Cost of 1000 Multiplication Operations (sec): | ||||
|---|---|---|---|---|
| FFA Bitness | Ch.9 "Soft" Comba | Ch.9 "Iron" Comba | Ch.10 Karatsuba (on Iron Comba) | Ch.11 Karatsuba (on Iron Comba) with Inlining |
| 2048 | 0.120 | 0.019 | 0.015 | 0.012 |
| 4096 | 0.480 | 0.074 | 0.046 | 0.035 |
| 8192 | 1.911 | 0.295 | 0.140 | 0.106 |
| 16384 | 7.638 | 1.170 | 0.427 | 0.328 |
The first item to discuss is that the introduction of ave1's new Musl GNAT had no measurable effect on the performance of the compiled FFA code.
Therefore the above benchmark does not list separate measurements for the new and old GNATs, as they turned out to build executables which perform identically within the margin of error given by the timer resolution.
This is not a particularly surprising discovery, given as the new GNAT is largely the same as the GNAT I had been using previously, but for the fact that it builds on Musl rather than rotten old glibc. Given as FFA spends no substantial time in libc, this observation is not astonishing.
At the same time I will note that all subsequent FFA tests will be carried out on the new GNAT, and the reader is advised to build himself a working copy.
However, ave1's inlining fix does have a measurable effect on performance: this is reflected in the smaller number of CPU cycles eaten by the FFA of Ch.11 compared to that of Ch.10.
The next item to discuss is the fact that the use of Mul_HalfWord_Soft in Word x Word multiplication imposes a substantial performance penalty.
Reader apeloyee was indeed correct: the slowdown was obscured in the modular exponentiation benchmark of Chapter 9 by the predominance of the modular reduction's cost over that of multiplication's. (This will be discussed in detail in Ch. 12B.)
On machines having a constant-time MUL instruction (e.g. AMD64) the use of "soft" Word x Word base case multiplication is an unnecessary sacrifice, and therefore the proclamation given in Chapter 9 is hereby withdrawn: people stuck with broken CPU architectures will be responsible for enabling the necessary workaround with their own hands, rather than imposing its cost on all FFA users.
At the conclusion of the FFA series, we will discuss a clean (i.e. via V-branches) means of offering the use of "soft" Word x Word multiplication on machines which require it, as well as a simple litmus test for the presence of a broken (i.e. one having a non-constant-time iron multiplier) CPU. But until then, all subsequent FFA benchmarks published here will presume the use of "Iron" Word x Word multiplication.
The last, and by far least surprising, observation concerning the benchmark is that Karatsuba multiplication is indeed faster (the exact runtime complexity of it -- I will leave as an exercise for the reader) for sufficiently large integers, than the Ch. 9 O(N^2) Comba method (the latter remains in use, however, as the base case of Karatsuba.)
At this time we will walk through the mechanics of our Karatsuba multiplier, so as to cement in the reader's head the correctness of the routine, and lay groundwork for the optimization which is introduced in Ch. 12B.
Let's revisit the Karatsuba routine, as given in Chapter 11:
fz_mul.adb:
-- ... -- Karatsuba's Multiplier. (CAUTION: UNBUFFERED) procedure Mul_Karatsuba(X : in FZ; Y : in FZ; XY : out FZ) is -- L is the wordness of a multiplicand. Guaranteed to be a power of two. L : constant Word_Count := X'Length; -- An 'LSeg' is the same length as either multiplicand. subtype LSeg is FZ(1 .. L); -- K is HALF of the length of a multiplicand. K : constant Word_Index := L / 2; -- A 'KSeg' is the same length as HALF of a multiplicand. subtype KSeg is FZ(1 .. K); -- The three L-sized variables of the product equation, i.e.: -- XY = LL + 2^(K*Bitness)(LL + HH + (-1^DD_Sub)*DD) + 2^(2*K*Bitness)HH LL, DD, HH : LSeg; -- K-sized terms of Dx * Dy = DD Dx, Dy : KSeg; -- Dx = abs(XLo - XHi) , Dy = abs(YLo - YHi) -- Subtraction borrows, signs of (XL - XH) and (YL - YH), Cx, Cy : WBool; -- so that we can calculate (-1^DD_Sub) -- Bottom and Top K-sized halves of the multiplicand X. XLo : KSeg renames X( X'First .. X'Last - K ); XHi : KSeg renames X( X'First + K .. X'Last ); -- Bottom and Top K-sized halves of the multiplicand Y. YLo : KSeg renames Y( Y'First .. Y'Last - K ); YHi : KSeg renames Y( Y'First + K .. Y'Last ); -- L-sized middle segment of the product XY (+/- K from the midpoint). XYMid : LSeg renames XY( XY'First + K .. XY'Last - K ); -- Bottom and Top L-sized halves of the product XY. XYLo : LSeg renames XY( XY'First .. XY'Last - L ); XYHi : LSeg renames XY( XY'First + L .. XY'Last ); -- Topmost K-sized quarter segment of the product XY, or 'tail' XYHiHi : KSeg renames XYHi( XYHi'First + K .. XYHi'Last ); -- Whether the DD term is being subtracted. DD_Sub : WBool; -- Carry from individual term additions. C : WBool; -- Tail-Carry accumulator, for the final ripple TC : Word; begin -- Recurse: LL := XL * YL FZ_Multiply_Unbuffered(XLo, YLo, LL); -- Recurse: HH := XH * YH FZ_Multiply_Unbuffered(XHi, YHi, HH); -- Dx := |XL - XH| , Cx := Borrow (i.e. 1 iff XL < XH) FZ_Sub_Abs(X => XLo, Y => XHi, Difference => Dx, Underflow => Cx); -- Dy := |YL - YH| , Cy := Borrow (i.e. 1 iff YL < YH) FZ_Sub_Abs(X => YLo, Y => YHi, Difference => Dy, Underflow => Cy); -- Recurse: DD := Dx * Dy FZ_Multiply_Unbuffered(Dx, Dy, DD); -- Whether (XL - XH)(YL - YH) is positive, and so DD must be subtracted: DD_Sub := 1 - (Cx xor Cy); -- XY := LL + 2^(2 * K * Bitness) * HH XYLo := LL; XYHi := HH; -- XY += 2^(K * Bitness) * HH, but carry goes in Tail Carry accum. FZ_Add_D(X => XYMid, Y => HH, Overflow => TC); -- XY += 2^(K * Bitness) * LL, ... FZ_Add_D(X => XYMid, Y => LL, Overflow => C); -- ... but the carry goes into the Tail Carry accumulator. TC := TC + C; -- XY += 2^(K * Bitness) * (-1^DD_Sub) * DD FZ_Not_Cond_D(N => DD, Cond => DD_Sub); -- invert DD if 2s-complementing FZ_Add_D(OF_In => DD_Sub, -- ... and then must increment X => XYMid, Y => DD, Overflow => C); -- carry will go in Tail Carry accumulator -- Compute the final Tail Carry for the ripple TC := TC + C - DD_Sub; -- Barring a cosmic ray, 0 < = TC <= 2 . pragma Assert(TC <= 2); -- Ripple the Tail Carry into the tail. FZ_Add_D_W(X => XYHiHi, W => TC, Overflow => C); -- Barring a cosmic ray, the tail ripple will NOT overflow. pragma Assert(C = 0); end Mul_Karatsuba; -- CAUTION: Inlining prohibited for Mul_Karatsuba ! -- Multiplier. (CAUTION: UNBUFFERED) procedure FZ_Multiply_Unbuffered(X : in FZ; Y : in FZ; XY : out FZ) is -- The length of either multiplicand L : constant Word_Count := X'Length; begin if L < = Karatsuba_Thresh then -- Base case: FZ_Mul_Comba(X, Y, XY); else -- Recursive case: Mul_Karatsuba(X, Y, XY); end if; end FZ_Multiply_Unbuffered; |
And now let's step through the whole thing, in light of the arithmetical overview given in Chapter 10.
Recall that we derived the following equivalences for Karatsuba's method:
LL = XLoYLo
HH = XHiYHi
Dx = |XLo - XHi|
Dy = |YLo - YHi|
DD = Dx × Dy
DDSub = CX XNOR CY
XY = LL + 2b(LL + HH + (-1DDSub)DD) + 22bHH
... where XLo and XHi are the bottom and top halves of the multiplicand X, respectively; YLo and YHi -- of multiplicand Y; CX is the subtraction "borrow" resulting from the computation of Dx; and CY is same from the computation of Dy.
... and showed that the operation can be represented in the following "physical" form (junior bits of registers on left hand side, senior -- on right hand) :
| LL | HH | TC := 0 | ||||
| + | LL | TC += Carry | ||||
| + | HH | TC += Carry | ||||
| + | (-1DDSub)DD | TC += Carry - DDSub | ||||
| + | TC | |||||
| = | XY | |||||
Now let's go through the routine itself and see which moving parts of the Ada program correspond to which pieces of the equivalence. And so, we begin at the beginning:
-- Karatsuba's Multiplier. (CAUTION: UNBUFFERED) procedure Mul_Karatsuba(X : in FZ; Y : in FZ; XY : out FZ) is |
X and Y, naturally, are the multiplicands; XY is the register to which the result of the multiplication is to be written. Observe that in the procedure's declaration:
fz_mul.ads:
-- ... -- Karatsuba's Multiplier. (CAUTION: UNBUFFERED) procedure Mul_Karatsuba(X : in FZ; Y : in FZ; XY : out FZ) with Pre => X'Length = Y'Length and XY'Length = (X'Length + Y'Length) and X'Length mod 2 = 0; -- CAUTION: Inlining prohibited for Mul_Karatsuba ! |
... it is mandated that the length of XY must suffice to hold the resulting integer; and that the length of each multiplicand must be divisible by two. (Recall that valid FZ integers must in fact be of lengths which constitute powers of 2; the reason for this will become evident shortly.)
We have thereby obtained the "physical" representation shown earlier in Ch. 10:
| XLo | XHi | |||||
| × | YLo | YHi | ||||
| = | XY | |||||
Let's proceed:
-- L is the wordness of a multiplicand. Guaranteed to be a power of two. L : constant Word_Count := X'Length; -- An 'LSeg' is the same length as either multiplicand. subtype LSeg is FZ(1 .. L); |
L is simply the length of either multiplicand (they are required, as shown in the declaration, to be of equal lengths.) K then corresponds to half of the length of a multiplicand; by breaking apart the multiplicands we will achieve the "divide and conquer" effect of Karatsuba's method, whereby we convert one multiplication of size 2K x 2K into three multiplications of size K x K.
Thereby L is the bit width of the
| XLo | XHi | |||
... and
| YLo | YHi | |||
... multiplicand registers; and as for K:
-- K is HALF of the length of a multiplicand. K : constant Word_Index := L / 2; -- A 'KSeg' is the same length as HALF of a multiplicand. subtype KSeg is FZ(1 .. K); |
K is the bit width of the low and high halves of the multiplicand registers, i.e. XLo, XHi, YLo, and YHi. Now we define the working registers for the intermediate terms in the equation:
-- The three L-sized variables of the product equation, i.e.: -- XY = LL + 2^(K*Bitness)(LL + HH + (-1^DD_Sub)*DD) + 2^(2*K*Bitness)HH LL, DD, HH : LSeg; -- K-sized terms of Dx * Dy = DD Dx, Dy : KSeg; -- Dx = abs(XLo - XHi) , Dy = abs(YLo - YHi) |
... let's also "draw to scale" all of these registers, and describe their desired eventual contents, referring to the earlier equivalences:
LL = XLoYLo
| XLo | ||
| x | YLo | |
| LL | ||
HH = XHiYHi
| XHi | ||
| x | YHi | |
| HH | ||
Dx = |XLo - XHi|
| XLo | |
| |-| | XHi |
| = | |
| Dx |
Dy = |YLo - YHi|
| YLo | |
| |-| | YHi |
| = | |
| Dy |
DD = Dx × Dy
| Dx | ||
| x | Dy | |
| = | ||
| DD | ||
Observe that DD is of width L, as FFA multiplication always results in an output having the summed width of the two multiplicands.
Now for Cx and Cy:
-- Subtraction borrows, signs of (XL - XH) and (YL - YH), Cx, Cy : WBool; -- so that we can calculate (-1^DD_Sub) |
These are simply the borrows recorded from the computation of Dx and Dy, we will need them when computing DD_Sub later on. Moving on:
-- Bottom and Top K-sized halves of the multiplicand X. XLo : KSeg renames X( X'First .. X'Last - K ); XHi : KSeg renames X( X'First + K .. X'Last ); -- Bottom and Top K-sized halves of the multiplicand Y. YLo : KSeg renames Y( Y'First .. Y'Last - K ); YHi : KSeg renames Y( Y'First + K .. Y'Last ); |
We already described these, they are the upper and lower halves of X and Y, i.e. the multiplicands.
Now, the middle term, XYMid:
-- L-sized middle segment of the product XY (+/- K from the midpoint). XYMid : LSeg renames XY( XY'First + K .. XY'Last - K ); |
XYMid is where we will be putting... (ignore TC for now...)
| + | LL | TC += Carry | ||||
| + | HH | TC += Carry | ||||
| + | (-1DDSub)DD | TC += Carry - DDSub | ||||
... i.e. the "middle" terms. It represents a "slice" of the multiplication's output register XY. But in order to represent the first term of the equivalence,
| LL | HH | TC := 0 | ||||
... we will also need to represent top and bottom "slices" of the output XY:
-- Bottom and Top L-sized halves of the product XY. XYLo : LSeg renames XY( XY'First .. XY'Last - L ); XYHi : LSeg renames XY( XY'First + L .. XY'Last ); |
Lastly, we will require a K-sized "slice" representation of XY, where we will be rippling out the accumulated "tail" carry, TC:
-- Topmost K-sized quarter segment of the product XY, or 'tail' XYHiHi : KSeg renames XYHi( XYHi'First + K .. XYHi'Last ); |
| + | TC | |||||
| = | XY | |||||
... when we complete the computation of the product XY.
As for:
-- Whether the DD term is being subtracted. DD_Sub : WBool; -- Carry from individual term additions. C : WBool; -- Tail-Carry accumulator, for the final ripple TC : Word; |
... we have already described them above, so let's:
begin |
And compute term LL:
-- Recurse: LL := XL * YL FZ_Multiply_Unbuffered(XLo, YLo, LL); |
LL = XLoYLo
| XLo | ||
| x | YLo | |
| LL | ||
... and then term HH:
-- Recurse: HH := XH * YH FZ_Multiply_Unbuffered(XHi, YHi, HH); |
HH = XHiYHi
| XHi | ||
| x | YHi | |
| HH | ||
Observe that we have begun to recurse: the invocations of multiplication may result in another Karatsubaization, or alternatively in an invocation of the Comba base case, depending on whether Karatsuba_Thresh is crossed; as specified in:
-- Multiplier. (CAUTION: UNBUFFERED) procedure FZ_Multiply_Unbuffered(X : in FZ; Y : in FZ; XY : out FZ) is -- The length of either multiplicand L : constant Word_Count := X'Length; begin if L < = Karatsuba_Thresh then -- Base case: FZ_Mul_Comba(X, Y, XY); else -- Recursive case: Mul_Karatsuba(X, Y, XY); end if; end FZ_Multiply_Unbuffered; |
The constant for the base case transition was determined empirically, and its optimal value appears to be the same on all machine architectures. However, the reader is invited to carry out his own experiments.
We have performed out two of our three recursions; we now want Dx:
Dx = |XLo - XHi|
| XLo | |
| |-| | XHi |
| = | |
| Dx |
-- Dx := |XL - XH| , Cx := Borrow (i.e. 1 iff XL < XH) FZ_Sub_Abs(X => XLo, Y => XHi, Difference => Dx, Underflow => Cx); |
... and Dy:
Dy = |YLo - YHi|
| YLo | |
| |-| | YHi |
| = | |
| Dy |
-- Dy := |YL - YH| , Cy := Borrow (i.e. 1 iff YL < YH) FZ_Sub_Abs(X => YLo, Y => YHi, Difference => Dy, Underflow => Cy); |
It is now time to show how FZ_Sub_Abs works:
fz_arith.adb:
-- Destructive: If Cond is 1, NotN := ~N; otherwise NotN := N. procedure FZ_Not_Cond_D(N : in out FZ; Cond : in WBool)is -- The inversion mask Inv : constant Word := 0 - Cond; begin for i in N'Range loop -- Invert (or, if Cond is 0, do nothing) N(i) := N(i) xor Inv; end loop; end FZ_Not_Cond_D; -- Subtractor that gets absolute value if underflowed, in const. time procedure FZ_Sub_Abs(X : in FZ; Y : in FZ; Difference : out FZ; Underflow : out WBool) is O : Word := 0; pragma Unreferenced(O); begin -- First, we subtract normally FZ_Sub(X, Y, Difference, Underflow); -- If borrow - negate, FZ_Not_Cond_D(Difference, Underflow); -- ... and also increment. FZ_Add_D_W(Difference, Underflow, O); end FZ_Sub_Abs; |
FZ_Sub_Abs is simply a constant-time means of taking the absolute value of a subtraction, and saving the output along with any resulting "borrow" bit for possible later use. Take careful note of the FZ_Not_Cond_D mechanism, you will be seeing it again shortly. The "D" stands for "Destructive" -- by this convention we refer to internal routines in FFA which operate "in-place", directly modifying their operand.
Moving on, we now want DD:
DD = Dx × Dy
| Dx | ||
| x | Dy | |
| = | ||
| DD | ||
-- Recurse: DD := Dx * Dy FZ_Multiply_Unbuffered(Dx, Dy, DD); |
And we got it -- with our third and final recursive call. Now we want DD_Sub:
-- Whether (XL - XH)(YL - YH) is positive, and so DD must be subtracted: DD_Sub := 1 - (Cx xor Cy); |
Why this is a valid equation for DD_Sub, is shown in a lemma in Chapter 10; please refer to it if memory fails you. Moving on to the upper and lower XY subterms,
| LL | HH | TC := 0 | ||||
-- XY := LL + 2^(2 * K * Bitness) * HH
XYLo := LL;
XYHi := HH; |
... and now let's begin to compute the middle term, XYMid:
| + | LL | TC += Carry | ||||
| + | HH | TC += Carry | ||||
-- XY += 2^(K * Bitness) * HH, but carry goes in Tail Carry accum. FZ_Add_D(X => XYMid, Y => HH, Overflow => TC); -- XY += 2^(K * Bitness) * LL, ... FZ_Add_D(X => XYMid, Y => LL, Overflow => C); -- ... but the carry goes into the Tail Carry accumulator. TC := TC + C; |
Observe that we accumulate the additions' carries in TC. But that's not all for the middle term, we also need the third subterm of it:
| + | (-1DDSub)DD | TC += Carry - DDSub | ||||
And we get it like this:
-- XY += 2^(K * Bitness) * (-1^DD_Sub) * DD FZ_Not_Cond_D(N => DD, Cond => DD_Sub); -- invert DD if 2s-complementing FZ_Add_D(OF_In => DD_Sub, -- ... and then must increment X => XYMid, Y => DD, Overflow => C); -- carry will go in Tail Carry accumulator |
We have already described FZ_Not_Cond_D; now it is necessary to review FZ_Add_D:
fz_arith.adb:
-- Destructive Add: X := X + Y; Overflow := Carry; optional OF_In procedure FZ_Add_D(X : in out FZ; Y : in FZ; Overflow : out WBool; OF_In : in WBool := 0) is Carry : WBool := OF_In; begin for i in 0 .. Word_Index(X'Length - 1) loop declare A : constant Word := X(X'First + i); B : constant Word := Y(Y'First + i); S : constant Word := A + B + Carry; begin X(X'First + i) := S; Carry := W_Carry(A, B, S); end; end loop; Overflow := Carry; end FZ_Add_D; |
This is simply "in-place" addition, economizing on stack space and CPU cycles by avoiding the use of an intermediate scratch register. Note that the mechanism is entirely agnostic of the particular element enumeration of the operand arrays -- this is required because we are operating on array slices, on which Ada wisely preserves the parent array's indexing.
Now we will compute the final "tail carry", TC, and ripple it into the final output of the multiplication, XY:
| + | TC | |||||
| = | XY | |||||
-- Compute the final Tail Carry for the ripple TC := TC + C - DD_Sub; -- Barring a cosmic ray, 0 < = TC <= 2 . pragma Assert(TC <= 2); -- Ripple the Tail Carry into the tail. FZ_Add_D_W(X => XYHiHi, W => TC, Overflow => C); -- Barring a cosmic ray, the tail ripple will NOT overflow. pragma Assert(C = 0); |
The proof regarding the validity of the ripple equation is given in Chapter 10, the reader is again asked to review it if the correctness of the given mechanism is not obvious to him.
Observe that we take a "belt and suspenders" approach regarding the correct operation of the carry ripple mechanism. Conceivably the asserts may be omitted in a speed-critical application; but their cost appears to be too small to measure on my system, and so they are to remain in the canonical version of FFA.
And, lastly,
end Mul_Karatsuba; -- CAUTION: Inlining prohibited for Mul_Karatsuba ! |
... naturally it is not permissible to inline a Karatsuba invocation, as the procedure is recursive.
We have now obtained the entire "sandwich" from earlier:
| LL | HH | TC := 0 | ||||
| + | LL | TC += Carry | ||||
| + | HH | TC += Carry | ||||
| + | (-1DDSub)DD | TC += Carry - DDSub | ||||
| + | TC | |||||
| = | XY | |||||
... i.e. the 2L-sized product XY of the L-sized multiplicands X and Y, having done so via three half-L-sized multiplications and a number of inexpensive additions/subtractions.
Satisfy yourself that at no point does the program branch on any bit inside the operands X and Y (i.e. it operates in constant time), and that the required stack memory and the depth of the recursion depend strictly on the FFA bitness set during invocation of FFACalc.
At this point you, dear reader, will have fit FFA multiplication into your head!
In Chapter 12B, we will examine an important special case of Karatsuba that merits a separate routine: squaring. Theoretically this operation requires only half of the CPU cycles demanded by the general case; and as it is made heavy use of in modular exponentiation:
-- Modular Exponent: Result := Base^Exponent mod Modulus procedure FZ_Mod_Exp(Base : in FZ; Exponent : in FZ; Modulus : in FZ; Result : out FZ) is -- Working register for the squaring; initially is copy of Base B : FZ(Base'Range) := Base; -- Copy of Exponent, for cycling through its bits E : FZ(Exponent'Range) := Exponent; -- Register for the Mux operation T : FZ(Result'Range); -- Buffer register for the Result R : FZ(Result'Range); begin -- Result := 1 WBool_To_FZ(1, R); -- For each bit of R width: for i in 1 .. FZ_Bitness(R) loop -- T := Result * B mod Modulus FZ_Mod_Mul(X => R, Y => B, Modulus => Modulus, Product => T); -- Sel is the current low bit of E; -- When Sel=0 -> Result := Result; -- When Sel=1 -> Result := T FZ_Mux(X => R, Y => T, Result => R, Sel => FZ_OddP(E)); -- Advance to the next bit of E FZ_ShiftRight(E, E, 1); -- B := B*B mod Modulus FZ_Mod_Mul(X => B, Y => B, Modulus => Modulus, Product => B); end loop; -- Output the Result: Result := R; end FZ_Mod_Exp; end FZ_ModEx; |
... we will find that the squaring-case of Karatsuba merits inclusion in FFA.
We will also make use of a simple means of profiling the execution of the FFA routines -- one that is unique in its simplicity, while generally inapplicable to heathen cryptographic libraries on account of their failure to avoid branching on operand bits.
~To be continued!~


