“Finite Field Arithmetic.” Chapter 12B: Karatsuba Redux. (Part 2 of 2)

Published on: Thursday November 22 2018

This article is part of a series of hands-on tutorials introducing FFA, or the Finite Field Arithmetic library. FFA differs from the typical "Open Sores" abomination, in that -- rather than trusting the author blindly with their lives -- prospective users are expected to read and fully understand every single line. In exactly the same manner that you would understand and pack your own parachute. The reader will assemble and test a working FFA with his own hands, and at the same time grasp the purpose of each moving part therein.

You will need:

Add the above vpatch and seal to your V-set, and press to ffa_ch12_karatsuba_redux.kv.vpatch.

You should end up with the same directory structure as previously.

Now compile ffacalc:

cd ffacalc
gprbuild

But do not run it quite yet.

This is where we will wrap up the subject of multiplication, and thereafter introduce no major changes to the respective routines, until the concluding chapters of the FFA series -- where we will discuss optional platform-specific optimizations.

Is the algorithmic cost of integer squaring the same as that of multiplication?

Intuitively it seems that calculating a b-bit X2 ought to be cheaper than multiplying a b-bit X by a b-bit Y, where X ≠ Y. But just how much cheaper? Let's find out.

Consider this trivial lemma:


For all integers x, y:

(x + y)2 - (x - y)2 = 4xy

From this, it follows that the product of any b-bit X and b-bit Y could be expressed as two squarings, one addition, two subtractions, and a division by 4 (i.e. bit-shift right by two places.)

Therefore a squaring has at least half the cost of a multiplication. This is a lower bound, i.e. it is demonstrably impossible for squaring to be asymptotically cheaper than multiplication by a factor greater than two -- since any multiplication can be expressed as a difference of two squares.

However, in physical practice, we will find that squarings costs somewhat more than half of what multiplications cost: there are similar constant (O(1)) and linear (O(b)) expense factors that go into setting the stage for either process.

There is also the fact that (x + y) is a b+1-bit quantity, making for a gnarly impedance mismatch with our "all integers will have power-of-two bit lengths" dictum.

And therefore we will not be rewriting all FFA integer multiplication in terms of difference-of-squares. But we will have a reasonably-optimized squaring routine, given as it is a quite-common operation (in, e.g. modular exponentiation.) Let's see how close to the theoretical minimum its cost can be brought.

Review the Karatsuba equivalences given in Chapter 12A:


LL = XLoYLo
HH = XHiYHi

Dx = |XLo - XHi|
Dy = |YLo - YHi|

DD = Dx × Dy

DDSub = CX XNOR CY

XY = LL + 2b(LL + HH + (-1DDSub)DD) + 22bHH

Now, let Y = X. Consequently:


LL = XLoXLo
HH = XHiXHi

Dx = |XLo - XHi|
DD = Dx2

... elementarily. And as for:


DDSub = CX XNOR CX

... now permanently equals 1, no matter what, and therefore we no longer need to care about the value of CX, the "borrow" bit from computing Dx. And so we get the following equation for Karatsuba's squaring:



XX = LL + 2b(LL + HH - DD) + 22bHH

Let's now make the "tasty sandwich" illustration of this equation, in the style of chapters 10 and 12A: (as before, junior bits of registers are on the left hand side, senior -- on right hand) :

LL HH TC := 0
+ LL TC += Carry
+ HH TC += Carry
- DD TC -= Borrow
+ TC
= XX

And just as before, we know that:


LL + HH >= DD

Therefore, at the time of the final carry ripple, it will always remain true that 0 < = TC <= 2, i.e. it will never be necessary to ripple a "borrow" into the senior-most quarter of the result XX.

We can now confidently write a Karatsuba's Squaring routine. But first, let's introduce a few necessary parts:

FZ_Sub_D is quite similar to the FZ_Add_D discussed in chapter Chapter 12A; but here, we subtract, rather than add, in-place:

fz_arith.adb:

   -- ...
 
   -- Destructive Sub: X := X - Y; Underflow := Borrow
   procedure FZ_Sub_D(X          : in out FZ;
                      Y          : in     FZ;
                      Underflow  : out    WBool) is
      Borrow : WBool := 0;
   begin
      for i in 0 .. Word_Index(X'Length - 1) loop
         declare
            A : constant Word := X(X'First + i);
            B : constant Word := Y(Y'First + i);
            S : constant Word := A - B - Borrow;
         begin
            X(X'First + i) := S;
            Borrow         := W_Borrow(A, B, S);
         end;
      end loop;
      Underflow := Borrow;
   end FZ_Sub_D;

We will also dispense with the pragma Assert mechanism for enforcing the mandatory nullity of the carry after the final TC ripple-out, in favour of this cleanly-adatronic device:

words.ads:

   -- ...
   -- For when a computed Word is mandatorily expected to equal zero:
   subtype WZeroOrDie is Word range 0 .. 0;

Any assignment of a value other than zero to a variable of this ranged subtype will trigger a CONSTRAINT_ERROR exception, signaling a catastrophic failure (of your iron! -- there is no other way that this can happen) -- and bring the program to a full stop.

Likewise, we will use a similar ranged subtype for enforcing the 0 < = TC <= 2 constraint. (And, note, the chapter 12B version of regular Karatsuba multiplication has been brought into conformance with this style.) The pieces in question are identical in the regular and squaring forms of Karatsuba: 

      -- Barring a cosmic ray, 0 < = TC <= 2
      subtype TailCarry is Word range 0 .. 2;
 
      -- Tail-Carry accumulator, for the final ripple-out into XXHiHi
      TC         : TailCarry := 0;
 
      -- Barring a cosmic ray, the tail ripple will NOT overflow.
      FinalCarry : WZeroOrDie := 0;

And now we can make the entire Karatsuba's Squaring routine: 

   -- Karatsuba's Squaring. (CAUTION: UNBUFFERED)
   procedure Sqr_Karatsuba(X  : in  FZ;
                           XX : out FZ) is
 
      -- L is the wordness of X. Guaranteed to be a power of two.
      L : constant Word_Count := X'Length;
 
      -- An 'LSeg' is the same length as X.
      subtype LSeg is FZ(1 .. L);
 
      -- K is HALF of the length of X.
      K : constant Word_Index := L / 2;
 
      -- A 'KSeg' is the same length as HALF of X.
      subtype KSeg is FZ(1 .. K);
 
      -- The three L-sized variables of the product equation, i.e.:
      -- XX = LL + 2^(K*Bitness)(LL + HH - DD) + 2^(2*K*Bitness)HH
      LL, DD, HH : LSeg;
 
      -- K-sized term Dx, Dx := abs(XLo - XHi) to then get DD := Dx^2
      Dx         : KSeg;
 
      -- IGNORED Subtraction borrow, sign of (XL - XH)
      Cx         : WBool; -- given as DD := Dx^2, DD is always positive
      pragma Unreferenced(Cx);
 
      -- Bottom and Top K-sized halves of X.
      XLo        : KSeg  renames    X(    X'First       ..    X'Last - K );
      XHi        : KSeg  renames    X(    X'First + K   ..    X'Last     );
 
      -- L-sized middle segment of the product XX (+/- K from the midpoint).
      XXMid      : LSeg  renames   XX(   XX'First + K   ..   XX'Last - K );
 
      -- Bottom and Top L-sized halves of the product XX.
      XXLo       : LSeg  renames   XX(   XX'First       ..   XX'Last - L );
      XXHi       : LSeg  renames   XX(   XX'First + L   ..   XX'Last     );
 
      -- Topmost K-sized quarter segment of the product XX, or 'tail'
      XXHiHi     : KSeg  renames XXHi( XXHi'First + K   .. XXHi'Last     );
 
      -- Carry from addition of HH and LL terms; borrow from subtraction of DD
      C          : WBool;
 
      -- Barring a cosmic ray, 0 < = TC <= 2
      subtype TailCarry is Word range 0 .. 2;
 
      -- Tail-Carry accumulator, for the final ripple-out into XXHiHi
      TC         : TailCarry := 0;
 
      -- Barring a cosmic ray, the tail ripple will NOT overflow.
      FinalCarry : WZeroOrDie := 0;
 
   begin
 
      -- Recurse: LL := XLo^2
      FZ_Square_Unbuffered(XLo, LL);
 
      -- Recurse: HH := XHi^2
      FZ_Square_Unbuffered(XHi, HH);
 
      -- Dx := |XLo - XHi| , and we don't care about the borrow
      FZ_Sub_Abs(X => XLo, Y => XHi, Difference => Dx, Underflow => Cx);
 
      -- Recurse: DD := Dx^2 (always positive, which is why we don't need Cx)
      FZ_Square_Unbuffered(Dx, DD);
 
      -- XX := LL + 2^(2 * K * Bitness) * HH
      XXLo := LL;
      XXHi := HH;
 
      -- XX += 2^(K * Bitness) * HH, carry goes into Tail Carry accumulator.
      FZ_Add_D(X => XXMid, Y => HH, Overflow => TC);
 
      -- XX += 2^(K * Bitness) * LL, ...
      FZ_Add_D(X => XXMid, Y => LL, Overflow => C);
 
      -- ... add the carry from LL addition into the Tail Carry accumulator.
      TC := TC + C;
 
      -- XX -= 2^(K * Bitness) * DD
      FZ_Sub_D(X         => XXMid, -- Because DD is always positive,
               Y         => DD,    -- this term is always subtractive.
               Underflow => C); -- C is the borrow from DD term subtraction
 
      -- Get final Tail Carry for the ripple by subtracting DD term's borrow
      TC := TC - C;
 
      -- Ripple the Tail Carry into the tail.
      FZ_Add_D_W(X => XXHiHi, W => TC, Overflow => FinalCarry);
 
   end Sqr_Karatsuba;
   -- CAUTION: Inlining prohibited for Sqr_Karatsuba !


We will not be "chewing apart" Sqr_Karatsuba -- it is closely analogous to the Chapter 12A item, which the reader is presumed to have fully grasped.

Naturally, this Karatsuba will need its own base case logic for the recursive invocations (as we cannot use the one from FZ_Mul) : 

   -- Squaring. (CAUTION: UNBUFFERED)
   procedure FZ_Square_Unbuffered(X     : in  FZ;
                                  XX    : out FZ) is
   begin
 
      if X'Length < = Sqr_Karatsuba_Thresh then
 
         -- Base case:
         FZ_Mul.FZ_Mul_Comba(X, X, XX);
 
      else
 
         -- Recursive case:
         Sqr_Karatsuba(X, XX);
 
      end if;
 
   end FZ_Square_Unbuffered;

... and a proper bufferization wrapper: 

   -- Squaring. Preserves the inputs.
   procedure FZ_Square_Buffered(X     : in  FZ;
                                XX_Lo : out FZ;
                                XX_Hi : out FZ) is
 
      -- Product buffer.
      P : FZ(1 .. 2 * X'Length);
 
   begin
 
      FZ_Square_Unbuffered(X, P);
 
      XX_Lo := P(P'First            .. P'First + X'Length - 1);
      XX_Hi := P(P'First + X'Length .. P'Last);
 
   end FZ_Square_Buffered;

But if you were to build this program, you would observe that the resulting squaring routine has a barely-detectable CPU-economy win over regular Karatsuba, i.e. Mul_Karatsuba(X => X, Y => X, XY => XX). Why?

The obvious answer is: most of the CPU cost of Karatsuba is paid in the base case. And so, here is what we really want: 

   procedure FZ_Square_Unbuffered(X     : in  FZ;
                                  XX    : out FZ) is
   begin
 
      if X'Length < = Sqr_Karatsuba_Thresh then
 
         -- Base case:
         FZ_Sqr_Comba(X, XX);
 
      else
 
         -- Recursive case:
         Sqr_Karatsuba(X, XX);
 
      end if;
 
   end FZ_Square_Unbuffered;

That is, we would like a specialized FZ_Sqr_Comba base case mechanism, which would take maximal advantage of the fact that we are computing X2 rather than X x Y, X ≠ Y.

To find an approach to this problem, let's begin by reviewing our ordinary Comba's Multiplication routine:

fz_mul.adb: 

   -- Comba's multiplier. (CAUTION: UNBUFFERED)
   procedure FZ_Mul_Comba(X     : in  FZ;
                          Y     : in  FZ;
                          XY    : out FZ) is
 
      -- Words in each multiplicand
      L : constant Word_Index := X'Length;
 
      -- Length of Product, i.e. double the length of either multiplicand
      LP : constant Word_Index := 2 * L;
 
      -- 3-word Accumulator
      A2, A1, A0 : Word := 0;
 
      -- Type for referring to a column of XY
      subtype ColXY is Word_Index range 0 .. LP - 1;
 
      -- Compute the Nth (indexed from zero) column of the Product
      procedure Col(N : in ColXY; U : in ColXY; V : in ColXY) is
 
         -- The outputs of a Word multiplication
         Lo, Hi : Word;
 
         -- Carry for the Accumulator addition
         C      : WBool;
 
         -- Sum for Accumulator addition
         Sum    : Word;
 
      begin
 
         -- For lower half of XY, will go from 0 to N
         -- For upper half of XY, will go from N - L + 1 to L - 1
         for j in U .. V loop
 
            -- Hi:Lo := j-th Word of X  *  (N - j)-th Word of Y
            Mul_Word(X(X'First + j),
                     Y(Y'First - j + N),
                     Lo, Hi);
 
            -- Now add Hi:Lo into the Accumulator:
 
            -- A0 += Lo; C := Carry
            Sum := A0 + Lo;
            C   := W_Carry(A0, Lo, Sum);
            A0  := Sum;
 
            -- A1 += Hi + C; C := Carry
            Sum := A1 + Hi + C;
            C   := W_Carry(A1, Hi, Sum);
            A1  := Sum;
 
            -- A2 += A2 + C
            A2  := A2 + C;
 
         end loop;
 
         -- We now have the Nth (indexed from zero) word of XY
         XY(XY'First + N) := A0;
 
         -- Right-Shift the Accumulator by one Word width:
         A0 := A1;
         A1 := A2;
         A2 := 0;
 
      end Col;
      pragma Inline_Always(Col);
 
   begin
 
      -- Compute the lower half of the Product:
      for i in 0 .. L - 1 loop
 
         Col(i, 0, i);
 
      end loop;
 
      -- Compute the upper half (sans last Word) of the Product:
      for i in L .. LP - 2 loop
 
         Col(i, i - L + 1, L - 1);
 
      end loop;
 
      -- The very last Word of the Product:
      XY(XY'Last) := A0;
 
   end FZ_Mul_Comba;

FZ_Mul_Comba is a quite simple mechanism, and the reader is expected to have understood it in Chapter 9. The product XY is obtained by computing columnwise, starting from the junior-most Word of XY, and proceeding through to the senior-most; carry from each columnar summation is found in the accumulator A2:A1:A0 after the Word-sized right shift, and gets added to the next column.

Now STOP! and... time for an exercise:

Chapter 12B Exercise #1:

Is it possible for A2:A1:A0 to overflow? And could this happen in Ch.12B FFA ? If not, why not?

Now let's suppose that we were to invoke the ordinary FZ_Mul_Comba on an X and Y consisting of 16 Words each, to produce a 32-Word XY product. This will not ordinarily happen in FFA, given our setting for the Karatsuba base case transition knob, but the illustration remains valid.

And let's also suppose that Y = X. The astute reader already anticipates that a certain portion of the work performed by ordinary FZ_Mul_Comba on such an input is redundant. So let's find out exactly where, so that we can conceive of a method for eliminating the redundancy.

Let's trace the execution of FZ_Mul_Comba in the above example. In square brackets, we will show which indices of multiplicands X and Y (arrays indexed from 1, in this illustration) are subjected to Mul_Word in a particular instance of the inner loop; N is the current column of the product being calculated.

We will mark in green all instances where an optimized Word x Word squaring ought to be taking place. And we will mark in yellow all cases where a Word x Word multiplication takes place unnecessarily, given as integer multiplication is commutative and we already have access to the result of that particular multiplication.

First, we trace the computation of the first half of the Comba X x X multiplication, i.e.: 

      -- Compute the lower half of the Product:
      for i in 0 .. L - 1 loop
 
         Col(i, 0, i);
 
      end loop;

And we get:


for i in 0 .. 16 - 1 loop
N=0; for j in 0 .. 0 loop
0 [ 1 x 1 ]

N=1; for j in 0 .. 1 loop
0 [ 1 x 2 ]
1 [ 2 x 1 ]

N=2; for j in 0 .. 2 loop
0 [ 1 x 3 ]
1 [ 2 x 2 ]
2 [ 3 x 1 ]

N=3; for j in 0 .. 3 loop
0 [ 1 x 4 ]
1 [ 2 x 3 ]
2 [ 3 x 2 ]
3 [ 4 x 1 ]

N=4; for j in 0 .. 4 loop
0 [ 1 x 5 ]
1 [ 2 x 4 ]
2 [ 3 x 3 ]
3 [ 4 x 2 ]
4 [ 5 x 1 ]

N=5; for j in 0 .. 5 loop
0 [ 1 x 6 ]
1 [ 2 x 5 ]
2 [ 3 x 4 ]
3 [ 4 x 3 ]
4 [ 5 x 2 ]
5 [ 6 x 1 ]

N=6; for j in 0 .. 6 loop
0 [ 1 x 7 ]
1 [ 2 x 6 ]
2 [ 3 x 5 ]
3 [ 4 x 4 ]
4 [ 5 x 3 ]
5 [ 6 x 2 ]
6 [ 7 x 1 ]

N=7; for j in 0 .. 7 loop
0 [ 1 x 8 ]
1 [ 2 x 7 ]
2 [ 3 x 6 ]
3 [ 4 x 5 ]
4 [ 5 x 4 ]
5 [ 6 x 3 ]
6 [ 7 x 2 ]
7 [ 8 x 1 ]

N=8; for j in 0 .. 8 loop
0 [ 1 x 9 ]
1 [ 2 x 8 ]
2 [ 3 x 7 ]
3 [ 4 x 6 ]
4 [ 5 x 5 ]
5 [ 6 x 4 ]
6 [ 7 x 3 ]
7 [ 8 x 2 ]
8 [ 9 x 1 ]

N=9; for j in 0 .. 9 loop
0 [ 1 x 10 ]
1 [ 2 x 9 ]
2 [ 3 x 8 ]
3 [ 4 x 7 ]
4 [ 5 x 6 ]
5 [ 6 x 5 ]
6 [ 7 x 4 ]
7 [ 8 x 3 ]
8 [ 9 x 2 ]
9 [ 10 x 1 ]

N=10; for j in 0 .. 10 loop
0 [ 1 x 11 ]
1 [ 2 x 10 ]
2 [ 3 x 9 ]
3 [ 4 x 8 ]
4 [ 5 x 7 ]
5 [ 6 x 6 ]
6 [ 7 x 5 ]
7 [ 8 x 4 ]
8 [ 9 x 3 ]
9 [ 10 x 2 ]
10 [ 11 x 1 ]

N=11; for j in 0 .. 11 loop
0 [ 1 x 12 ]
1 [ 2 x 11 ]
2 [ 3 x 10 ]
3 [ 4 x 9 ]
4 [ 5 x 8 ]
5 [ 6 x 7 ]
6 [ 7 x 6 ]
7 [ 8 x 5 ]
8 [ 9 x 4 ]
9 [ 10 x 3 ]
10 [ 11 x 2 ]
11 [ 12 x 1 ]

N=12; for j in 0 .. 12 loop
0 [ 1 x 13 ]
1 [ 2 x 12 ]
2 [ 3 x 11 ]
3 [ 4 x 10 ]
4 [ 5 x 9 ]
5 [ 6 x 8 ]
6 [ 7 x 7 ]
7 [ 8 x 6 ]
8 [ 9 x 5 ]
9 [ 10 x 4 ]
10 [ 11 x 3 ]
11 [ 12 x 2 ]
12 [ 13 x 1 ]

N=13; for j in 0 .. 13 loop
0 [ 1 x 14 ]
1 [ 2 x 13 ]
2 [ 3 x 12 ]
3 [ 4 x 11 ]
4 [ 5 x 10 ]
5 [ 6 x 9 ]
6 [ 7 x 8 ]
7 [ 8 x 7 ]
8 [ 9 x 6 ]
9 [ 10 x 5 ]
10 [ 11 x 4 ]
11 [ 12 x 3 ]
12 [ 13 x 2 ]
13 [ 14 x 1 ]

N=14; for j in 0 .. 14 loop
0 [ 1 x 15 ]
1 [ 2 x 14 ]
2 [ 3 x 13 ]
3 [ 4 x 12 ]
4 [ 5 x 11 ]
5 [ 6 x 10 ]
6 [ 7 x 9 ]
7 [ 8 x 8 ]
8 [ 9 x 7 ]
9 [ 10 x 6 ]
10 [ 11 x 5 ]
11 [ 12 x 4 ]
12 [ 13 x 3 ]
13 [ 14 x 2 ]
14 [ 15 x 1 ]

N=15; for j in 0 .. 15 loop
0 [ 1 x 16 ]
1 [ 2 x 15 ]
2 [ 3 x 14 ]
3 [ 4 x 13 ]
4 [ 5 x 12 ]
5 [ 6 x 11 ]
6 [ 7 x 10 ]
7 [ 8 x 9 ]
8 [ 9 x 8 ]
9 [ 10 x 7 ]
10 [ 11 x 6 ]
11 [ 12 x 5 ]
12 [ 13 x 4 ]
13 [ 14 x 3 ]
14 [ 15 x 2 ]
15 [ 16 x 1 ]

Now, we trace the execution of the second half of the X x X computation, i.e.: 

      -- Compute the upper half (sans last Word) of the Product:
      for i in L .. LP - 2 loop
 
         Col(i, i - L + 1, L - 1);
 
      end loop;

And we get:


for i in 16 .. 2 * 16 - 2 loop

N=16; for j in 1 .. 15 loop
1 [ 2 x 16 ]
2 [ 3 x 15 ]
3 [ 4 x 14 ]
4 [ 5 x 13 ]
5 [ 6 x 12 ]
6 [ 7 x 11 ]
7 [ 8 x 10 ]
8 [ 9 x 9 ]
9 [ 10 x 8 ]
10 [ 11 x 7 ]
11 [ 12 x 6 ]
12 [ 13 x 5 ]
13 [ 14 x 4 ]
14 [ 15 x 3 ]
15 [ 16 x 2 ]

N=17; for j in 2 .. 15 loop
2 [ 3 x 16 ]
3 [ 4 x 15 ]
4 [ 5 x 14 ]
5 [ 6 x 13 ]
6 [ 7 x 12 ]
7 [ 8 x 11 ]
8 [ 9 x 10 ]
9 [ 10 x 9 ]
10 [ 11 x 8 ]
11 [ 12 x 7 ]
12 [ 13 x 6 ]
13 [ 14 x 5 ]
14 [ 15 x 4 ]
15 [ 16 x 3 ]

N=18; for j in 3 .. 15 loop
3 [ 4 x 16 ]
4 [ 5 x 15 ]
5 [ 6 x 14 ]
6 [ 7 x 13 ]
7 [ 8 x 12 ]
8 [ 9 x 11 ]
9 [ 10 x 10 ]
10 [ 11 x 9 ]
11 [ 12 x 8 ]
12 [ 13 x 7 ]
13 [ 14 x 6 ]
14 [ 15 x 5 ]
15 [ 16 x 4 ]

N=19; for j in 4 .. 15 loop
4 [ 5 x 16 ]
5 [ 6 x 15 ]
6 [ 7 x 14 ]
7 [ 8 x 13 ]
8 [ 9 x 12 ]
9 [ 10 x 11 ]
10 [ 11 x 10 ]
11 [ 12 x 9 ]
12 [ 13 x 8 ]
13 [ 14 x 7 ]
14 [ 15 x 6 ]
15 [ 16 x 5 ]

N=20; for j in 5 .. 15 loop
5 [ 6 x 16 ]
6 [ 7 x 15 ]
7 [ 8 x 14 ]
8 [ 9 x 13 ]
9 [ 10 x 12 ]
10 [ 11 x 11 ]
11 [ 12 x 10 ]
12 [ 13 x 9 ]
13 [ 14 x 8 ]
14 [ 15 x 7 ]
15 [ 16 x 6 ]

N=21; for j in 6 .. 15 loop
6 [ 7 x 16 ]
7 [ 8 x 15 ]
8 [ 9 x 14 ]
9 [ 10 x 13 ]
10 [ 11 x 12 ]
11 [ 12 x 11 ]
12 [ 13 x 10 ]
13 [ 14 x 9 ]
14 [ 15 x 8 ]
15 [ 16 x 7 ]

N=22; for j in 7 .. 15 loop
7 [ 8 x 16 ]
8 [ 9 x 15 ]
9 [ 10 x 14 ]
10 [ 11 x 13 ]
11 [ 12 x 12 ]
12 [ 13 x 11 ]
13 [ 14 x 10 ]
14 [ 15 x 9 ]
15 [ 16 x 8 ]

N=23; for j in 8 .. 15 loop
8 [ 9 x 16 ]
9 [ 10 x 15 ]
10 [ 11 x 14 ]
11 [ 12 x 13 ]
12 [ 13 x 12 ]
13 [ 14 x 11 ]
14 [ 15 x 10 ]
15 [ 16 x 9 ]

N=24; for j in 9 .. 15 loop
9 [ 10 x 16 ]
10 [ 11 x 15 ]
11 [ 12 x 14 ]
12 [ 13 x 13 ]
13 [ 14 x 12 ]
14 [ 15 x 11 ]
15 [ 16 x 10 ]

N=25; for j in 10 .. 15 loop
10 [ 11 x 16 ]
11 [ 12 x 15 ]
12 [ 13 x 14 ]
13 [ 14 x 13 ]
14 [ 15 x 12 ]
15 [ 16 x 11 ]

N=26; for j in 11 .. 15 loop
11 [ 12 x 16 ]
12 [ 13 x 15 ]
13 [ 14 x 14 ]
14 [ 15 x 13 ]
15 [ 16 x 12 ]

N=27; for j in 12 .. 15 loop
12 [ 13 x 16 ]
13 [ 14 x 15 ]
14 [ 15 x 14 ]
15 [ 16 x 13 ]

N=28; for j in 13 .. 15 loop
13 [ 14 x 16 ]
14 [ 15 x 15 ]
15 [ 16 x 14 ]

N=29; for j in 14 .. 15 loop
14 [ 15 x 16 ]
15 [ 16 x 15 ]

N=30; for j in 15 .. 15 loop
15 [ 16 x 16 ]

And, of course, the final Word of the result is obtained by: 

      -- The very last Word of the Product:
      XY(XY'Last) := A0;

So we find precisely what we expected to find: nearly half of the CPU work taken up by an invocation of ordinary FZ_Mul_Comba on two identical multiplicands, is avoidable. So now let's take a shot at avoiding it, by writing a new Comba squaring subroutine: 

   -- Square case of Comba's multiplier. (CAUTION: UNBUFFERED)
   procedure FZ_Sqr_Comba(X  : in  FZ;
                          XX : out FZ) is
 
      -- Words in each multiplicand
      L : constant Word_Index := X'Length;
 
      -- Length of Product, i.e. double the length of X
      LP : constant Word_Index := 2 * L;
 
      -- 3-word Accumulator
      A2, A1, A0 : Word := 0;
 
      Lo, Hi  : Word; -- Output of WxW multiply/square
 
      -- Type for referring to a column of XX
      subtype ColXX is Word_Index range 0 .. LP - 1;
 
      procedure Accum is
         C      : WBool; -- Carry for the Accumulator addition
         Sum    : Word;  -- Sum for Accumulator addition
      begin
         -- Now add add double-Word Hi:Lo to accumulator A2:A1:A0:
         -- A0 += Lo; C := Carry
         Sum := A0 + Lo;
         C   := W_Carry(A0, Lo, Sum);
         A0  := Sum;
         -- A1 += Hi + C; C := Carry
         Sum := A1 + Hi + C;
         C   := W_Carry(A1, Hi, Sum);
         A1  := Sum;
         -- A2 += A2 + C
         A2  := A2 + C;
      end Accum;
      pragma Inline_Always(Accum);
 
      procedure SymmDigits(N : in ColXX; From : in ColXX; To : in ColXX) is
      begin
         for j in From .. To loop
            -- Hi:Lo := j-th * (N - j)-th Word, and then,
            Mul_Word(X(X'First + j),
                     X(X'First - j + N),
                     Lo, Hi);
            Accum;
            Accum; -- Accum += 2 * (Hi:Lo)
         end loop;
      end SymmDigits;
      pragma Inline_Always(SymmDigits);
 
      procedure SqrDigit(N : in ColXX) is
      begin
         Sqr_Word(X(X'First + N), Lo, Hi); -- Hi:Lo := Square(N-th digit)
         Accum;                            -- Accum += Hi:Lo
      end SqrDigit;
      pragma Inline_Always(SqrDigit);
 
      procedure HaveDigit(N : in ColXX) is
      begin
         -- Save the Nth (indexed from zero) word of XX:
         XX(XX'First + N) := A0;
         -- Right-Shift the Accumulator by one Word width:
         A0 := A1;
         A1 := A2;
         A2 := 0;
      end HaveDigit;
      pragma Inline_Always(HaveDigit);
 
      -- Compute the Nth (indexed from zero) column of the Product
      procedure Col(N : in ColXX; U : in ColXX; V : in ColXX) is
      begin
         -- The branch pattern depends only on FZ wordness
         if N mod 2 = 0 then         -- If we're doing an EVEN-numbered column:
            SymmDigits(N, U, V - 1); --   Stop before V: it is the square case
            SqrDigit(V);             --   Compute the square case at V
         else                        -- If we're doing an ODD-numbered column:
            SymmDigits(N, U, V);     --   All of them are the symmetric case
         end if;                     -- After either even or odd column:
         HaveDigit(N);               --   We have the N-th digit of the result.
      end Col;
      pragma Inline_Always(Col);
 
   begin
      -- First col always exists:
      SqrDigit(ColXX'First);
      HaveDigit(ColXX'First);
 
      -- Compute the lower half of the Product:
      for i in 1 .. L - 1 loop
         Col(i, 0, i / 2);
      end loop;
 
      -- Compute the upper half (sans last Word) of the Product:
      for i in L .. LP - 2 loop
         Col(i, i - L + 1, i / 2);
      end loop;
 
      -- The very last Word of the Product:
      XX(XX'Last) := A0; -- Equiv. of XX(XX'First + 2*L - 1) := A0;
   end FZ_Sqr_Comba;

This variant correctly isolates the Word x Word squarings, and avoids carrying out the symmetrically-redundant Word x Word multiplications.

Now STOP! and... time for an exercise:

Chapter 12B Exercise #2:

Prove that the conditional branch statement in the Col routine: 

         if N mod 2 = 0 then         -- If we're doing an EVEN-numbered column:
            SymmDigits(N, U, V - 1); --   Stop before V: it is the square case
            SqrDigit(V);             --   Compute the square case at V
         else                        -- If we're doing an ODD-numbered column:
            SymmDigits(N, U, V);     --   All of them are the symmetric case
         end if;                     -- ...

... does not entail a branch on secret bits, i.e. an act that would violate the constant-time guarantee offered by the FFA system.

Done with the exercise? Let's carry on...

Notice anything missing? Of course, it's Sqr_Word -- we haven't defined it yet. So let's define it.

First, take a look at our existing portable Word x Word multiplier, Mul_Word:

w_mul.adb:

   -- Carry out X*Y mult, return lower word XY_LW and upper word XY_HW.
   procedure Mul_Word(X       : in  Word;
                      Y       : in  Word;
                      XY_LW   : out Word;
                      XY_HW   : out Word) is
 
      -- Bottom half of multiplicand X
      XL : constant HalfWord := BottomHW(X);
 
      -- Top half of multiplicand X
      XH : constant HalfWord := TopHW(X);
 
      -- Bottom half of multiplicand Y
      YL : constant HalfWord := BottomHW(Y);
 
      -- Top half of multiplicand Y
      YH : constant HalfWord := TopHW(Y);
 
      -- XL * YL
      LL : constant Word := Mul_HalfWord_Iron(XL, YL);
 
      -- XL * YH
      LH : constant Word := Mul_HalfWord_Iron(XL, YH);
 
      -- XH * YL
      HL : constant Word := Mul_HalfWord_Iron(XH, YL);
 
      -- XH * YH
      HH : constant Word := Mul_HalfWord_Iron(XH, YH);
 
      -- Carry
      CL : constant Word := TopHW(TopHW(LL) + BottomHW(LH) + BottomHW(HL));
 
   begin
 
      -- Get the bottom half of the Product:
      XY_LW := LL + Shift_Left(LH + HL, HalfBitness);
 
      -- Get the top half of the Product:
      XY_HW := HH + TopHW(HL) + TopHW(LH) + CL;
 
   end Mul_Word;

And now we will want to make a similar and equally-portable Word-squaring operator: 

   ---------------------------------------------------------------------------
   -- LET A CURSE FALL FOREVER on the authors of GCC, and on the Ada committee,
   -- neither of whom saw it fit to decree a primitive which returns both
   -- upper and lower halves of an iron MUL instruction's result. Consequently,
   -- portable Mul_Word demands ~four~ MULs (and several additions and shifts);
   -- while portable Sqr_Word demands ~three~ MULs (and likewise adds/shifts.)
   -- If it were not for their idiocy, BOTH routines would weigh 1 CPU instr.!
   ---------------------------------------------------------------------------
 
   -- Carry out X*X squaring, return lower word XX_LW and upper word XX_HW.
   procedure Sqr_Word(X       : in  Word;
                      XX_LW   : out Word;
                      XX_HW   : out Word) is
 
      -- Bottom half of multiplicand X
      XL : constant HalfWord := BottomHW(X);
 
      -- Top half of multiplicand X
      XH : constant HalfWord := TopHW(X);
 
      -- XL^2
      LL : constant Word := Mul_HalfWord_Iron(XL, XL);
 
      -- XL * XH
      LH : constant Word := Mul_HalfWord_Iron(XL, XH);
 
      -- XH^2
      HH : constant Word := Mul_HalfWord_Iron(XH, XH);
 
      -- Carry
      CL : constant Word := TopHW(TopHW(LL) + Shift_Left(BottomHW(LH), 1));
 
   begin
 
      -- Get the bottom half of the Product:
      XX_LW := LL + Shift_Left(LH, HalfBitness + 1);
 
      -- Get the top half of the Product:
      XX_HW := HH + Shift_Left(TopHW(LH), 1) + CL;
 
   end Sqr_Word;

Satisfy yourself that this works, and only then proceed.

Now, we'll naturally want to find out what, if anything, all of these new moving parts achieve.

So let's add a squaring operator to our old friend ffacalc:

ffa_calc.adb:

               -- ...
               ---------------------------------------------------------
               -- Ch. 12B:
               -- Square, give bottom and top halves
            when 'S' =>
               Want(1);
               Push;
               FFA_FZ_Square(X     => Stack(SP - 1),
                             XX_Lo => Stack(SP - 1),
                             XX_Hi => Stack(SP));
               ---------------------------------------------------------

Now STOP! and... time for an exercise:

Chapter 12B Exercise #3:


a) Create a ffacalc tape which obtains a random number, squares it using the above mechanism, and verifies that the result is equal to the output of a squaring carried out via ordinary multiplication.


b) Given the fact that your RNG (supposing it is a genuine TRNG!) is not able to produce output in constant time, how would you write the above tape such that you can verify that all of the squarings in fact take place in constant time? (Hint: ffacalc tapes can produce ffacalc tapes...)

Now let's run a Thousand Squares benchmark, on various FFA bitnesses -- including a few quite outrageous ones, by cryptographic standards:

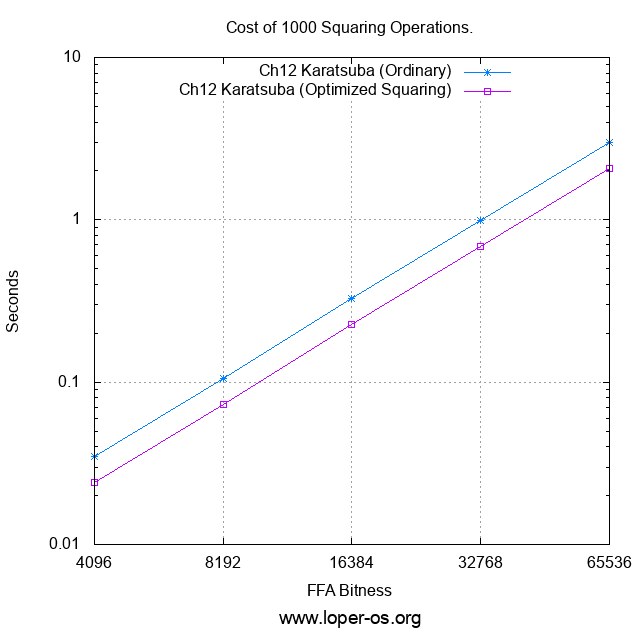
Cost of 1000 Squaring Operations, vs FFA Bitness.

Or, for those who prefer the raw numbers to the logarithmic plot,

Cost of 1000 Squaring Operations (sec):
FFA Bitness Ch.12B Karatsuba (Ordinary) Ch.12B Karatsuba (Optimized Squaring)
4096 0.035 0.024
8192 0.106 0.073
16384 0.328 0.226
32768 0.991 0.686
65536 3.000 2.080

It turns out that we have achieved a one-third reduction, vs. ordinary Karatsuba, in the cost of integer squaring.

It is possible to do better than this: a good chunk of the potential "win" from the optimized squaring, "evaporates" (on x86 and other common iron) into branch prediction friction inside FZ_Sqr_Comba, and into the wasteful Mul_Word and Sqr_Word portable Word x Word multipliers.

In the final chapters of the FFA series, we will consider some cures, including unrolled Comba multiplication and iron-specific inline ASM. These however will forever remain optional components -- as they are inevitably bought with significant cost to portability and clarity.

For now, we will stop here, and see what, if anything, our new optimized squaring method does to the cost of the king of expensive FFA operations: modular exponentiation (as used in e.g. RSA.)

So let's rewrite the Chapter 11 FZ_Mod_Exp to make use of Sqr_Karatsuba:

fz_modex.adb:

   -- Modular Squaring: Product := X*X mod Modulus
   procedure FZ_Mod_Sqr(X        : in  FZ;
                        Modulus  : in  FZ;
                        Product  : out FZ) is
 
      -- The wordness of both operands is equal:
      L     : constant Indices := X'Length;
 
      -- Double-width register for squaring and modulus operations
      XX    : FZ(1 .. L * 2);
 
      -- To refer to the lower and upper halves of the working register:
      XX_Lo : FZ renames XX(1     .. L);
      XX_Hi : FZ renames XX(L + 1 .. XX'Last);
 
   begin
 
      -- XX_Lo:XX_Hi := X^2
      FZ_Square_Buffered(X, XX_Lo, XX_Hi);
 
      -- Product := XX mod M
      FZ_Mod(XX, Modulus, Product);
 
   end FZ_Mod_Sqr;
 
 
   -- Modular Exponent: Result := Base^Exponent mod Modulus
   procedure FZ_Mod_Exp(Base     : in  FZ;
                        Exponent : in  FZ;
                        Modulus  : in  FZ;
                        Result   : out FZ) is
 
      -- Working register for the squaring; initially is copy of Base
      B : FZ(Base'Range)     := Base;
 
      -- Copy of Exponent, for cycling through its bits
      E : FZ(Exponent'Range) := Exponent;
 
      -- Register for the Mux operation
      T : FZ(Result'Range);
 
      -- Buffer register for the Result
      R : FZ(Result'Range);
 
   begin
      -- Result := 1
      WBool_To_FZ(1, R);
 
      -- For each bit of R width:
      for i in 1 .. FZ_Bitness(R) loop
 
         -- T := Result * B mod Modulus
         FZ_Mod_Mul(X => R, Y => B, Modulus => Modulus, Product => T);
 
         -- Sel is the current low bit of E;
         --    When Sel=0 -> Result := Result;
         --    When Sel=1 -> Result := T
         FZ_Mux(X => R, Y => T, Result => R, Sel => FZ_OddP(E));
 
         -- Advance to the next bit of E
         FZ_ShiftRight(E, E, 1);
 
         -- B := B^2 mod Modulus
         FZ_Mod_Sqr(X => B, Modulus => Modulus, Product => B);
 
      end loop;
 
      -- Output the Result:
      Result := R;
 
   end FZ_Mod_Exp;

... and then perform the familiar "RSA benchmark", a la Chapter 9:

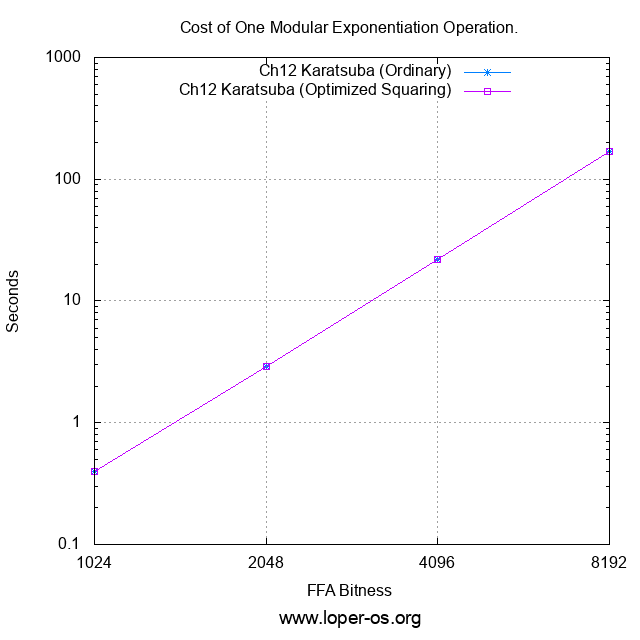
Cost of 1 Modular Exponentiation Operation, vs FFA Bitness.

Or, for those who prefer the raw numbers to the logarithmic plot,

Cost of One Modular Exponentiation Operation (sec):
FFA Bitness Ch.12B Karatsuba (Ordinary) Ch.12B Karatsuba (Optimized Squaring)
1024 0.395 0.395
2048 2.895 2.895
4096 21.920 21.895
8192 169.729 169.394

It would appear that optimized squaring had virtually no effect! ...to the limit of the timer resolution!

It ought to be mentioned that the resolution of the timer used here is quite poor, i.e. it is the customary unix "time" command.

But let's find out what is happening! Recall the wunderwaffe that was promised to the reader in Chapter 12A:


"We will also make use of a simple means of profiling the execution of the FFA routines -- one that is unique in its simplicity, while generally inapplicable to heathen cryptographic libraries on account of their failure to avoid branching on operand bits."

And now recall that FFA operations do not branch on operand bits. This means, among other things, that it is possible to profile the execution of individual routines simply via selective nulling. Naturally, you will not obtain arithmetically-correct outputs from a thusly-mutilated FFA, but you will get a measure of the CPU cost of an individual component; nulling it out, provided that Gnat's optimizer is prevented from discarding anything else, will give an accurate approximation of a computation's cost minus that of the particular component.

So let's perform the necessary vivisections:

fz_modex.adb:

   -- Modular Multiply: Product := X*Y mod Modulus
   procedure FZ_Mod_Mul(X        : in  FZ;
                        Y        : in  FZ;
                        Modulus  : in  FZ;
                        Product  : out FZ) is
 
      -- The wordness of all three operands is equal:
      L     : constant Indices := X'Length;
 
      -- Double-width register for multiplication and modulus operations
      XY    : FZ(1 .. L * 2);
 
      -- To refer to the lower and upper halves of the working register:
      XY_Lo : FZ renames XY(1     .. L);
      XY_Hi : FZ renames XY(L + 1 .. XY'Last);
 
   begin
 
      -- XY_Lo:XY_Hi := X * Y
      FZ_Multiply_Buffered(X, Y, XY_Lo, XY_Hi);
 
      -- Product := XY mod M
      --  FZ_Mod(XY, Modulus, Product);
 
      Product := XY_Lo;
 
   end FZ_Mod_Mul;
 
 
   -- Modular Squaring: Product := X*X mod Modulus
   procedure FZ_Mod_Sqr(X        : in  FZ;
                        Modulus  : in  FZ;
                        Product  : out FZ) is
 
      -- The wordness of both operands is equal:
      L     : constant Indices := X'Length;
 
      -- Double-width register for squaring and modulus operations
      XX    : FZ(1 .. L * 2);
 
      -- To refer to the lower and upper halves of the working register:
      XX_Lo : FZ renames XX(1     .. L);
      XX_Hi : FZ renames XX(L + 1 .. XX'Last);
 
   begin
 
      -- XX_Lo:XX_Hi := X^2
      FZ_Square_Buffered(X, XX_Lo, XX_Hi);
 
      -- Product := XX mod M
      --  FZ_Mod(XX, Modulus, Product);
 
      Product := XX_Lo;
 
   end FZ_Mod_Sqr;

Naturally, this program will not produce a correct modular exponentiation output! But it does fool Gnat's optimizer, so that it will not drop the calls to FZ_Mod_Mul and FZ_Mod_Sqr, and so we can get a picture of what the effect of optimized squaring would be if the modular reduction step weren't there to drown out the signal.

And we get:

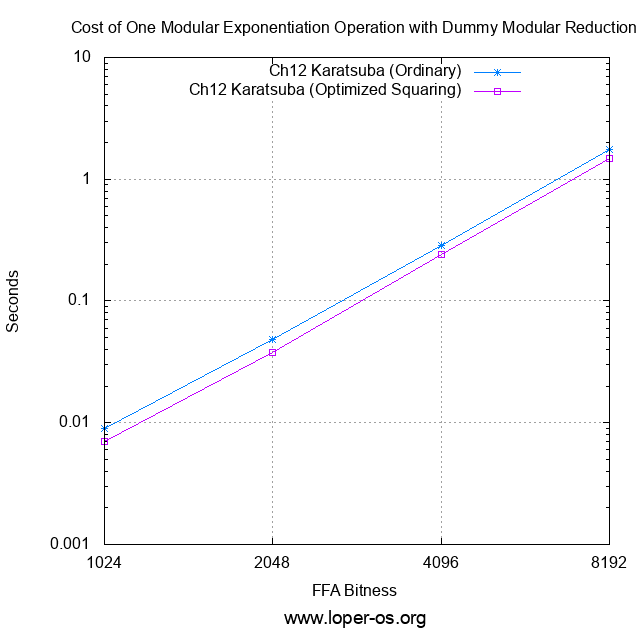
Cost of 1 Modular Exponentiation Operation, with Dummy Modular Reduction, vs FFA Bitness.

This experiment confirms that reader apeloyee was indeed correct: modular reduction in the form currently in use (Knuth's integer division method) -- is so outrageously expensive that it dwarfs the cost of all other components of FZ_Mod_Exp !


In Chapter 13, we will begin laying the groundwork for a modular reduction mechanism that is not hobbled by the use of the slow FZ_Mod Knuthian integer-division operation, and instead relies almost entirely on multiplication.

~To be continued!~
This entry was written by Stanislav , posted on Thursday November 22 2018 , filed under Ada, Bitcoin, Cold Air, Computation, Cryptography, FFA, Friends, Mathematics, ShouldersGiants, SoftwareArchaeology, SoftwareSucks . Bookmark the permalink . Post a comment below or leave a trackback: Trackback URL.

Leave a Reply

XHTML: You can use these tags: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong> <pre lang="" line="" escaped="" highlight="">


MANDATORY: Please prove that you are human:

74 xor 33 = ?

What is the serial baud rate of the FG device ?


Answer the riddle correctly before clicking "Submit", or comment will NOT appear! Not in moderation queue, NOWHERE!

« »