“Finite Field Arithmetic.” Chapter 14B: Barrett's Modular Reduction. (Part 2 of 2.)
This article is part of a series of hands-on tutorials introducing FFA, or the Finite Field Arithmetic library. FFA differs from the typical "Open Sores" abomination, in that -- rather than trusting the author blindly with their lives -- prospective users are expected to read and fully understand every single line. In exactly the same manner that you would understand and pack your own parachute. The reader will assemble and test a working FFA with his own hands, and at the same time grasp the purpose of each moving part therein.
- Chapter 1: Genesis.
- Chapter 2: Logical and Bitwise Operations.
- Chapter 3: Shifts.
- Chapter 4: Interlude: FFACalc.
- Chapter 5: "Egyptological" Multiplication and Division.
- Chapter 6: "Geological" RSA.
- Chapter 7: "Turbo Egyptians."
- Chapter 8: Interlude: Randomism.
- Chapter 9: "Exodus from Egypt" with Comba's Algorithm.
- Chapter 10: Introducing Karatsuba's Multiplication.
- Chapter 11: Tuning and Unified API.
- Chapter 12A: Karatsuba Redux. (Part 1 of 2)
- Chapter 12B: Karatsuba Redux. (Part 2 of 2)
- Chapter 13: "Width-Measure" and "Quiet Shifts."
- Chapter 14A: Barrett's Modular Reduction. (Part 1 of 2)
- Chapter 14A-Bis: Barrett's Modular Reduction. (Physical Bounds Proof.)
- Chapter 14B: Barrett's Modular Reduction. (Part 2 of 2.)
You will need:
- A Keccak-based VTron (for this and all subsequent chapters.)
- All of the materials from Chapters 1 - 14A-Bis.
- ffa_ch14_barrett.kv.vpatch
- ffa_ch14_barrett.kv.vpatch.asciilifeform.sig
Add the above vpatches and seals to your V-set, and press to ffa_ch14_barrett.kv.vpatch.
You should end up with the same directory structure as previously.
Now compile ffacalc:
cd ffacalc gprbuild |
But do not run it quite yet.
First, the mail bag!
Reader diana_coman recently observed that the OF_in parameter taken by certain procedures in FZ_Shift is not checked for validity, and -- if abused by being given an oversized (i.e. wider than the given shiftness) value -- could result in a garbage output.
Her observation is entirely correct. And ideally, the range of OF_in would be constrained via a precondition. Unfortunately, Ada does not permit the use of preconditions in combination with inlining; and FZ_Shift routines are invoked in several costly inner loops, and absolutely must be subject to inlining. Therefore, it is impractical to actually verify the bit-width of OF_in on every invocation. It is, however, the case that these procedures are defined strictly for internal use in FFA, and hence do not constitute a danger to the operator. After giving the matter some thought, I took diana_coman's suggestion and added comments to warn the reader of the potential rake he could step on if he were to insist on making direct use of FFA's internal shift routines.
I will take this opportunity to remind the reader that FFA is designed to be "safe if used as prescribed": if it is invoked via the provided external interface, the promised semantics are guaranteed to apply. The only prohibited operations are ones which over- or under-run the FFACalc stack, demand a division by zero, or attempt to violate other FFACalc rules. (These will bring the program to an orderly stop, and warn the operator.) All other actions will produce arithmetically-correct outputs for the given inputs. However it is impractical on extant iron to make this guarantee for each of the internal components taken separately!
This is why we want sane iron, with inexpensive bounds-checking instructions! But we do not have it yet. Hence, the reader who wishes to make use of FFA internals for some custom purpose of his own, must proceed with extreme caution.
Reader diana_coman also observed that Get_Argument in FFACalc's command line handler:
procedure Get_Argument(Number : in Natural; Result : out String); |
... can be turned into the stricter type:
procedure Get_Argument(Number : in Natural; Result : out CmdLineArg); |
I have included the change in this Chapter.
Thank you for these nitpicks, diana_coman! And for reading and signing Chapters 3, 4, 5, and 6:
- ffa_ch3_shifts.kv.vpatch.diana_coman.sig
- ffa_ch4_ffacalc.kv.vpatch.diana_coman.sig
- ffa_ch5_egypt.kv.vpatch.diana_coman.sig
- ffa_ch6_simplest_rsa.kv.vpatch.diana_coman.sig
Reader mircea_popescu observed that Chapter 13's FZ_Measure can be slightly simplified, where:
Index := W_Mux(Index + 1, Index, W_ZeroP(W)); |
... can be safely turned into the equivalent:
Index := Index + W_NZeroP(W); |
I have included the change in this Chapter. Thank you, reader mircea_popescu !
Now, let's eat the meat of this Chapter.
We'll start with a very minor extension of FFACalc. A Version command has been introduced:
| Op | Description | # Ins | # Outs | Notes |
|---|---|---|---|---|
| V | Put the FFACalc and FFA version numbers on the stack. | 0 | 2 | Kelvin Versioning is in use. |
The implementation of this command is quite straightforward:
-- Put the FFACalc Program Version on the stack, -- followed by FFA Program Version. when 'V' => Push; Push; -- FFACalc Version: FFA_FZ_Clear(Stack(SP - 1)); FFA_FZ_Set_Head(Stack(SP - 1), Word(FFACalc_K_Version)); -- FFA Version: FFA_FZ_Clear(Stack(SP)); FFA_FZ_Set_Head(Stack(SP), Word(FFA_K_Version)); |
package Version is pragma Pure; ---------------------------------------------- -- Current 'deg. Kelvin' Version of FFACalc -- ---------------------------------------------- FFACalc_K_Version : constant Natural := 255; ---------------------------------------------- end Version; |
-- ... ---------------------------------------------------------------------------- --- Current 'deg. Kelvin' Version of FFA ---------------------------------------------------------------------------- FFA_K_Version : constant Natural := 255; -- ... |
The effect: FFACalc and FFA now have independent "Degrees Kelvin" versions -- i.e. they are to decrement by one upon every published revision to each respective program. Observe that this constitutes a promise to the reader: no more than 255 changes to either FFACalc or FFA are to be published after this Chapter. In the quite unlikely event where a change is found to be required after a Kelvin version reaches zero degrees, it is expected that the program is to be renamed, Vtronically-reground, and some very pointed questions posed to the maintainer!
Now, let's proceed to the originally-planned subject of Chapter 14B: the Ada implementation of Barrett's Modular Reduction.

Don't even think about proceeding further into this Chapter if you have not fully read and understood the two previous chapters:
- The arithmetical proof of Barrett's Modular Reduction
- The physical bounds proof of Barrett's Modular Reduction
Stop now and go back, study! Lest you become a danger to yourself and others.
We will now discuss the Ada implementation of the Algorithm 2 given in Chapter 14A. Please print the Algorithm and the physical bounds proof and refer to these while reading this Chapter.
Let's start with the relatively-obvious:
package FZ_Barr is pragma Pure; -- Precomputed data for Barrett's Modular Reduction type Barretoid(ZXMLength : Indices; BarretoidLength : Indices) is record ZXM : FZ(1 .. ZXMLength); -- Zero-Extended Modulus J : FZBit_Index; -- Jm B : FZ(1 .. BarretoidLength); -- The Barrettoid itself ZSlide : FZBit_Index; -- Amount to slide Z Degenerate : WBool; -- Is it degenerate case? end record; -- Prepare the precomputed Barrettoid corresponding to a given Modulus procedure FZ_Make_Barrettoid(Modulus : in FZ; Result : out Barretoid) with Pre => Result.B'Length = 2 * Modulus'Length and Result.ZXM'Length = Modulus'Length + 1; -- Reduce N using the given precomputed Barrettoid. procedure FZ_Barrett_Reduce(X : in FZ; Bar : in Barretoid; XReduced : in out FZ); pragma Inline_Always(FZ_Barrett_Reduce); end FZ_Barr; |
In every instance of the pre-computed Barrettoid data structure, we will keep everything which is required for Barrett's Modular Reduction by a given modulus. In particular, we will retain ZXM: a zero-extended (for convenient use in steps 6 and 8) copy of the modulus itself; the parameter JM; the Barrettoid proper, BM; ZSlide, the number of bits we must right-shift Z by to compute ZS; and, finally, the degeneracy indicator, i.e. DM.
Unsurprisingly, a Barrettoid is computed from a given modulus with the procedure FZ_Make_Barrettoid. All Barrettoids -- like other FFA data -- will exist as stack-allocations. (Heapism in any form whatsoever is forever banned in FFA.) And the only use of a Barrettoid is to compute Barrett's Modular Reduction, using FZ_Barrett_Reduce. We will review both procedures in detail, below.
Here is how we create a Barrettoid:
-- Prepare the precomputed Barrettoid corresponding to a given Modulus procedure FZ_Make_Barrettoid(Modulus : in FZ; Result : out Barretoid) is -- Length of Modulus and Remainder Lm : constant Indices := Modulus'Length; -- Remainder register, starts as zero Remainder : FZ(1 .. Lm) := (others => 0); -- Length of Quotient, with an extra Word for top bit (if Degenerate) Lq : constant Indices := (2 * Lm) + 1; -- Valid indices into Quotient, using the above subtype Quotient_Index is Word_Index range 1 .. Lq; -- The Quotient we need, i.e. 2^(2 * ModulusBitness) / Modulus Quotient : FZ(Quotient_Index); -- Permissible 'cuts' for the Slice operation subtype Divisor_Cuts is Word_Index range 2 .. Lm; -- Current bit of Pseudo-Dividend; high bit is 1, all others 0 Pb : WBool := 1; -- Performs Restoring Division on a given segment procedure Slice(Index : Quotient_Index; Cut : Divisor_Cuts; Bits : Positive) is begin declare -- Borrow, from comparator C : WBool; -- Left-Shift Overflow LsO : WBool; -- Current cut of Remainder register Rs : FZ renames Remainder(1 .. Cut); -- Current cut of Divisor Ds : FZ renames Modulus(1 .. Cut); -- Current Word of Quotient being made, starting from the highest W : Word := 0; -- Current bit of Quotient (inverted) nQb : WBool; begin -- For each bit in the current Pseudo-Dividend Word: for b in 1 .. Bits loop -- Advance Rs, shifting in the current Pseudo-Dividend bit: FZ_ShiftLeft_O_I(N => Rs, ShiftedN => Rs, Count => 1, OF_In => Pb, -- Current Pseudo-Dividend bit Overflow => LsO); -- Subtract Divisor-Cut from R-Cut; Underflow goes into C: FZ_Sub(X => Rs, Y => Ds, Difference => Rs, Underflow => C); -- Negation of current Quotient bit nQb := C and W_Not(LsO); -- If C=1, the subtraction underflowed, and we must undo it: FZ_Add_Gated(X => Rs, Y => Ds, Sum => Rs, Gate => nQb); -- Save the bit of Quotient that we have found: W := Shift_Left(W, 1) or (1 - nQb); -- i.e. inverse of nQb end loop; -- We made a complete Word of the Quotient; save it: Quotient(Quotient'Last + 1 - Index) := W; -- Indexed from end end; end Slice; pragma Inline_Always(Slice); -- Measure of the Modulus ModulusMeasure : constant FZBit_Index := FZ_Measure(Modulus); begin -- First, process the high Word of the Pseudo-Dividend: Slice(1, 2, 1); -- ... it has just one bit: a 1 at the bottom position -- Once we ate the top 1 bit of Pseudo-Dividend, rest of its bits are 0 Pb := 0; -- Process the Modulus-sized segment below the top Word: for i in 2 .. Lm - 1 loop Slice(i, i + 1, Bitness); -- stay ahead by a word to handle carry end loop; -- Process remaining Words: for i in Lm .. Lq loop Slice(i, Lm, Bitness); end loop; -- Record the Quotient (i.e. the Barrettoid proper, Bm) Result.B := Quotient(Result.B'Range); -- Record whether we have the Degenerate Case (1 iff Modulus = 1) Result.Degenerate := W_NZeroP(Quotient(Lq)); -- Record a copy of the Modulus, extended with zero Word: Result.ZXM(Modulus'Range) := Modulus; Result.ZXM(Result.ZXM'Last) := 0; -- Record the parameter Jm: Result.J := ModulusMeasure - 1; -- Wm - Jm Result.ZSlide := FZBit_Index(Bitness * Modulus'Length) - ModulusMeasure + 1; end FZ_Make_Barrettoid; |
The process may seem complicated, but it is merely a specialized form of FZ_Mod. With the difference that we are interested in the quotient, rather the remainder, and also wish to compute certain additional parameters corresponding to the given modulus.
Recall that a Barrettoid BM for a given modulus M, was defined as the quantity ⌊2k / M⌋. In FZ_Make_Barrettoid, we compute it via Knuth's division. Afterwards we record: the modulus itself; the quotient; whether the given modulus corresponds to the degenerate case M = 1; the parameter JM; and the parameter ZSlide. After this, the contents of the Barrettoid can be used to perform modular reduction modulo M in constant time.
And now, let's show exactly how:
-- Reduce X using the given precomputed Barrettoid. procedure FZ_Barrett_Reduce(X : in FZ; Bar : in Barretoid; XReduced : in out FZ) is -- Wordness of X, the quantity being reduced Xl : constant Indices := X'Length; -- Wordness of XReduced (result), one-half of Xl, and same as of Modulus Ml : constant Indices := XReduced'Length; -- i.e. # of Words in Wm. -- The Modulus we will reduce X by Modulus : FZ renames Bar.ZXM(1 .. Ml); -- Shifted X Xs : FZ(X'Range); -- Z := Xs * Bm (has twice the length of X) Z : FZ(1 .. 2 * Xl); -- Upper 3Wm-bit segment of Z that gets shifted to form Zs ZHi : FZ renames Z(Ml + 1 .. Z'Last ); -- Middle 2Wm-bit segment of Z, that gets multiplied by M to form Q Zs : FZ renames Z(Z'First + Ml .. Z'Last - Ml ); -- Sub-terms of the Zs * M multiplication: ZsLo : FZ renames Zs(Zs'First .. Zs'Last - Ml ); ZsHi : FZ renames Zs(Zs'First + Ml .. Zs'Last ); ZsHiM : FZ(1 .. Ml); -- Q := Modulus * Zs, i.e. floor(X / M)*M + E*M Q : FZ(1 .. Xl); QHi : FZ renames Q(Q'First + Ml .. Q'Last ); -- R is made one Word longer than Modulus (see proof re: why) Rl : constant Indices := Ml + 1; -- Reduction estimate, overshot by 0, 1, or 2 multiple of Modulus R : FZ(1 .. Rl); -- Scratch for the outputs of the gated subtractions S : FZ(1 .. Rl); -- Borrow from the gated subtractions C : WBool; -- Barring cosmic ray, no underflow can take place in (4) and (5) NoCarry : WZeroOrDie := 0; begin -- Result is initially zero (and will stay zero if Modulus = 1) FZ_Clear(XReduced); -- (1) Ns := X >> Jm FZ_Quiet_ShiftRight(N => X, ShiftedN => Xs, Count => Bar.J); -- (2) Z := X * Bm FZ_Multiply_Unbuffered(X => Bar.B, Y => Xs, XY => Z); -- (3) Zs := Z >> 2Wm - Jm (already thrown lower Wm, so only Wm - Jm now) FZ_Quiet_ShiftRight(N => ZHi, ShiftedN => ZHi, Count => Bar.ZSlide); -- (4) Q := Zs * M (this is split into three operations, see below) -- ... first, Q := ZsLo * M, FZ_Multiply_Unbuffered(ZsLo, Modulus, Q); -- ... then, compute ZsHiM := ZsHi * M, FZ_Low_Multiply_Unbuffered(ZsHi, Modulus, ZsHiM); -- ... finally, add ZsHiM to upper half of Q. FZ_Add_D(X => QHi, Y => ZsHiM, Overflow => NoCarry); -- (5) R := X - Q (we only need Rl-sized segments of X and Q here) FZ_Sub(X => X(1 .. Rl), Y => Q(1 .. Rl), Difference => R, Underflow => NoCarry); -- (6) S1 := R - M, C1 := Borrow (1st gated subtraction of Modulus) FZ_Sub(X => R, Y => Bar.ZXM, Difference => S, Underflow => C); -- (7) R := {C1=0 -> S1, C1=1 -> R} FZ_Mux(X => S, Y => R, Result => R, Sel => C); -- (8) S2 := R - M, C2 := Borrow (2nd gated subtraction of Modulus) FZ_Sub(X => R, Y => Bar.ZXM, Difference => S, Underflow => C); -- (9) R := {C2=0 -> S2, C2=1 -> R} FZ_Mux(X => S, Y => R, Result => R, Sel => C); -- (10) RFinal := {DM=0 -> R, DM=1 -> 0} (handle the degenerate case) FZ_Mux(X => R(1 .. Ml), Y => XReduced, Result => XReduced, Sel => Bar.Degenerate); -- If Modulus = 1, then XReduced is 0. end FZ_Barrett_Reduce; |
Notice anything unfamiliar? The astute reader will observe that the above is an exact implementation of the process described in Chapter 14A-Bis; the only new subcomponent is the FZ_Low_Multiply_Unbuffered routine used in Step 4. So let's learn what it's made of.
But first, review the elementary multiplication equivalence from Chapter 10:
| XLo | XHi | ||||
| × | YLo | YHi | |||
| = | |||||
| XLoYLo | |||||
| + | XLoYHi | ||||
| + | XHiYLo | ||||
| + | XHiYHi | ||||
| = | XY | ||||
Suppose, however, that we were only interested in calculating the bottom half of XY. We can then write the following schematic instead:
| XLoYLo | |||
| + | (XLoYHi)Lo | ||
| + | (XHiYLo)Lo | ||
| = | XYLo | ||
Observe that this method is exactly analogous to the mechanism used in Chapter 9's Mul_Word, where we find the lower half of a Word × Word multiplication by:
-- ........ -- XL * YL LL : constant Word := Mul_HalfWord_Iron(XL, YL); -- XL * YH LH : constant Word := Mul_HalfWord_Iron(XL, YH); -- XH * YL HL : constant Word := Mul_HalfWord_Iron(XH, YL); -- ........ begin -- Get the bottom half of the Product: XY_LW := LL + Shift_Left(LH + HL, HalfBitness); -- ........ |
So let's now see how this works for FZ rather than Word:
-- "Low Multiplication" computes only the bottom half of the product XY. -- Presently, it is used solely in Barrett's Modular Reduction. package body FZ_LoMul is -- Low-Only Comba's multiplier. (CAUTION: UNBUFFERED) procedure FZ_Low_Mul_Comba(X : in FZ; Y : in FZ; XY : out FZ) is -- Words in each multiplicand (and also in the half-product) L : constant Word_Index := X'Length; -- 3-word Accumulator A2, A1, A0 : Word := 0; begin -- Compute the lower half of the Product, which is all we want: for N in 0 .. L - 1 loop -- Compute the Nth (indexed from zero) column of the Half-Product declare -- The outputs of a Word multiplication Lo, Hi : Word; -- Carry for the Accumulator addition C : WBool; -- Sum for Accumulator addition Sum : Word; begin -- For lower half of XY, will go from 0 to N -- For upper half of XY, will go from N - L + 1 to L - 1 for j in 0 .. N loop -- Hi:Lo := j-th Word of X * (N - j)-th Word of Y Mul_Word(X(X'First + j), Y(Y'First - j + N), Lo, Hi); -- Now add Hi:Lo into the Accumulator: -- A0 += Lo; C := Carry Sum := A0 + Lo; C := W_Carry(A0, Lo, Sum); A0 := Sum; -- A1 += Hi + C; C := Carry Sum := A1 + Hi + C; C := W_Carry(A1, Hi, Sum); A1 := Sum; -- A2 += A2 + C A2 := A2 + C; end loop; -- We now have the Nth (indexed from zero) word of XY XY(XY'First + N) := A0; -- Right-Shift the Accumulator by one Word width: A0 := A1; A1 := A2; A2 := 0; end; end loop; end FZ_Low_Mul_Comba; -- Low-Only Multiplier. (CAUTION: UNBUFFERED) procedure Low_Mul(X : in FZ; Y : in FZ; XY : out FZ) is -- L is the wordness of a multiplicand. Guaranteed to be a power of two. L : constant Word_Count := X'Length; -- K is HALF of the length of a multiplicand. K : constant Word_Index := L / 2; -- A 'KSeg' is the same length as HALF of a multiplicand. subtype KSeg is FZ(1 .. K); -- The two K-sized variables of the half-product equation: LH, HL : KSeg; -- Bottom and Top K-sized halves of the multiplicand X. XLo : KSeg renames X( X'First .. X'Last - K ); XHi : KSeg renames X( X'First + K .. X'Last ); -- Bottom and Top K-sized halves of the multiplicand Y. YLo : KSeg renames Y( Y'First .. Y'Last - K ); YHi : KSeg renames Y( Y'First + K .. Y'Last ); -- Top K-sized half of the half-product XY. XYHi : KSeg renames XY( XY'First + K .. XY'Last ); -- Carry from individual term additions. C : WBool; pragma Unreferenced(C); begin -- Recurse to FULL-width multiplication: XY := XLo * YLo FZ_Multiply_Unbuffered(XLo, YLo, XY); -- Recurse to HALF-width multiplication: LH := XLo * YHi FZ_Low_Multiply_Unbuffered(XLo, YHi, LH); -- Recurse to HALF-width multiplication: HL := XHi * YLo FZ_Low_Multiply_Unbuffered(XHi, YLo, HL); -- XY += 2^(K * Bitness) * LH FZ_Add_D(X => XYHi, Y => LH, Overflow => C); -- XY += 2^(K * Bitness) * HL FZ_Add_D(X => XYHi, Y => HL, Overflow => C); end Low_Mul; -- CAUTION: Inlining prohibited for Low_Mul ! -- Low-Only Multiplier. (CAUTION: UNBUFFERED) procedure FZ_Low_Multiply_Unbuffered(X : in FZ; Y : in FZ; XY : out FZ) is -- The length of either multiplicand L : constant Word_Count := X'Length; begin if L < = Low_Mul_Thresh then -- Base case: FZ_Low_Mul_Comba(X, Y, XY); else -- Recursive case: Low_Mul(X, Y, XY); end if; end FZ_Low_Multiply_Unbuffered; |
FZ_Low_Mul_Comba, of course, is merely a cut-down Comba from Chapter 9; while the recursion is analogous to the one in Chapter 10's Karatsuba and Chapter 12's Square Karatsuba.
Now, let's see where Barrett's Reduction is put to use. You will recall the conclusion of Chapter 12B, where we discussed the fact that the use of Knuth's division for modular reduction is quite expensive, and constitutes the bulk of the cost of modular exponentiation as presented in Chapters 6 through 13. And now, at last, we can write a fast modular reducer -- one that uses Barrett's method instead of Knuth's division:
-- (Barrettronic) Modular Exponent: Result := Base^Exponent mod Modulus procedure FZ_Mod_Exp(Base : in FZ; Exponent : in FZ; Modulus : in FZ; Result : out FZ) is -- Double-width scratch buffer for the modular operations D : FZ(1 .. Base'Length * 2); -- Working register for the squaring; initially is copy of Base B : FZ(Base'Range) := Base; -- Register for the Mux operation T : FZ(Result'Range); -- Buffer register for the Result R : FZ(Result'Range); -- Space for Barrettoid Bar : Barretoid(ZXMLength => Modulus'Length + 1, BarretoidLength => 2 * B'Length); begin -- First, pre-compute the Barretoid for the given Modulus: FZ_Make_Barrettoid(Modulus => Modulus, Result => Bar); -- Result := 1 WBool_To_FZ(1, R); -- For each Word of the Exponent: for i in Exponent'Range loop declare -- The current Word of the Exponent Wi : Word := Exponent(i); begin -- For each bit of Wi: for j in 1 .. Bitness loop -- T := Result * B mod Modulus FZ_Multiply_Unbuffered(X => R, Y => B, XY => D); FZ_Barrett_Reduce(X => D, Bar => Bar, XReduced => T); -- Sel is the current bit of Exponent; -- When Sel=0 -> Result := Result; -- When Sel=1 -> Result := T FZ_Mux(X => R, Y => T, Result => R, Sel => Wi and 1); -- Advance to the next bit of Wi (i.e. next bit of Exponent) Wi := Shift_Right(Wi, 1); -- B := B^2 mod Modulus FZ_Square_Unbuffered(X => B, XX => D); FZ_Barrett_Reduce(X => D, Bar => Bar, XReduced => B); end loop; end; end loop; -- Output the Result: Result := R; end FZ_Mod_Exp; |
Quite straightforward: we precompute the Barrettoid, and use it for all of the necessary modular multiplications and squarings modulo the given modulus.
The reader may be curious regarding how to properly test this program. And so I will invite him to download a complete package of test tapes, generated using a RNG:
- ch14_modexp_test_tapes.tar.gz (Warning: 22MB)
- ch14_modexp_test_tapes.tar.gz.asciilifeform.sig (PGP Signature)
Each modular exponentiation test tape was mechanically-produced on Chapter 13 FFA, and contains a series of modular exponentiations, each followed by an equality comparison with the expected result. E.g., a 2048-bit test:
.09C98FCB9C40EC96BB9ECE3FD053D8468614D2C262A6ED7ACC613968CAF8A58F
A725E113CCB16A000BF82170353B71789E23DD4620966EE23191C97F0290606CB
7AEF750CF9EB6716BB474BA28DD3A615D3FC3D19812ABB2735676C7EBD505497A
3080BF349F28335439FC0567C150006CE796D9F4307B0A5C0617619C0F4C29CB4
96D164F09E363A8D535149B3485D4D0F0C8F2395CBC8E067910CDD9A0228AE6E2
E37CA22F75EE91944C231899A1B340DB9968C6AB1EC7DBA911B0AF3CD3AD1AE83
573A51A7DAC53E8FFCBF9D985BE9CC003409ADB8E068CBE71243C4A4EB678D169
489FD0818B91C35F9A073DD2BC06173E13578481C1E98692B79C0A1CBB
.513C8694309772EA44FEA976BE4DD5674F0A798D20385E1F18D71ACA6FD1680D
9A09E9F075BEB7FE8A30911106618A4BC961CC0442E9BB8939D0CB249FEA16ECE
CB6762ADEFD1CD660842CDA6CF7EC2EF4C523E61E8F119A1357AF40DAE7E1ECE4
9F27C23728CD5186D197802AD03098ACFD8E058BD7F8340FFFB5E8ACB807D7B96
D223FB0EC6D6E68C01C6293BC94B5BD370888C192F9C62C617B1598B8F19914C5
F98DBB5B9D06936B5E97BDDE87FEB0192C9EB0A32D9F7B066D134FB5E9215FF24
40340DC33568F5F4441A25F040D81CF584923A7DF28135F5F30282D344278E60D
8DBCB0D36C8641057265406E31896C6BC15DB82F0BDAFC5F456C9EB35F
.1F8FF0E6C3FF3A40C18BBAB99D9DB19A6413C734507638D6F44B90848D7B4FE2
E87E4D830B14F03E7FD87F47CCD4A715C51839952C5DB5B3F04E4C9633964881B
761E763D745B5DF2F8649418CB4B3DCA692535B862FC2C62F11DCEE2AB4191B25
B35A6DEDC585476DACF952A2F580C061F9DCD6C0CE4F08BF401379EC47CED1DE5
A3C87EC98CE4DFFC70EB65A3C6700C5145107D3DD305BA1E0E0F6A957566A0452
BE16E39CF4A17185644FBA8ED1CA79A3D6E28D29D936F2F953913EFBB94B7AF0C
AA81CF3F5EF5C86E2F115424FEEEBD1DAD7FB371E27B2D727381F441ED5377E3D
AB15BCF786E88582D6533AF673FA86047EBBC1667E6A12DD7102359052
MX
.0FCB1DE435944F516B3F05D990C761985348076167AFCF56FEA05BE1DBA81286
BA2139B0D10232577B79A4B9B872244E966EDC256678D1132B206D357D90F1F60
1B663DFD62FE78449A0D1E4B7E7FC55C2B978282D37B70A6D8715451BC114282B
3E9555E23612C2974974FA52ADDC6F2B030F0E98E6C5C6747C23A58FAE4C8730A
37426B54EC604EA1EF16F24B1FE8B190A993FC28A95960987D1768AC731DEC4E6
B334C75B27589F0E99DAC4A7AC5CA9E7A014C2E0F05A72A18145A9B8958D0F26E
179D3854E3C8CD0C3DD8E11DA318F9BE873175B1168580CEA42593FEC2795FDBD
BC349D10B76118E646AA8EE5C2295452C2E78DC26528F7C4A4D2F90E21
={(do nothing if ok)}{[SAD ]}_ |
One invokes the tapes as follows, e.g. for the 1024-bit 10,000 shot tape:
$ time cat 10k_shots_1024bit_ffa_unif_rnd.tape | ./bin/ffa_calc 1024 32 |
... and if successful (i.e. all outputs are correct) it will emit only the output of the unix "time" command; e.g. on my test iron:
real 7m24.751s user 7m24.081s sys 0m0.290s |
Now, the reader has probably read Dijkstra and recalls that "testing can reveal the presence of bugs, but never their absence." So why bother? The answer is, it is necessary to test your iron.
The test tapes in the signed TAR come in two variants, slid (where there are randomly-sized stretches of leading zeroes in the arguments to modular exponentiation) and uniform -- where there are not. You can use the test tapes as a litmus of whether your iron provides a constant-time iron multiplier and a constant-time barrel shifter. If you find that the "slid" tapes reliably execute faster on your machine than the "unif" tapes of the same respective FFA width, you have sad iron and must enable the workarounds (i.e. Mul_HalfWord_Soft and/or HaveBarrelShifter := False.)
Now let's find out what we actually achieve by using Barrett's Reduction:
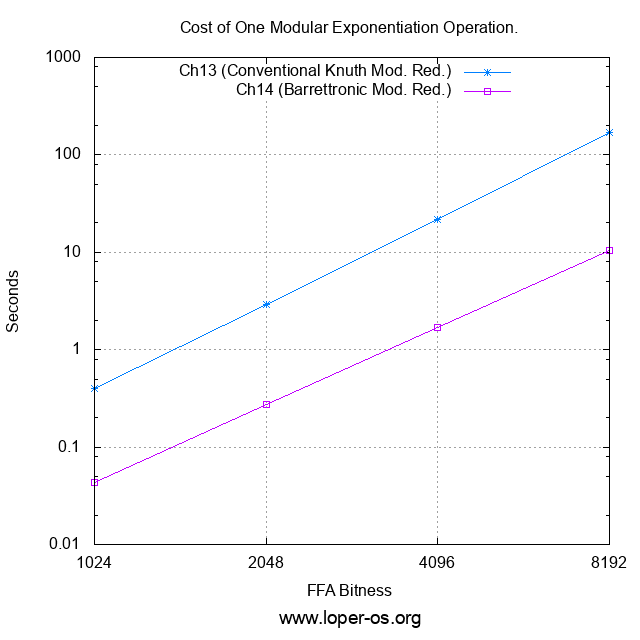
Or, for those who prefer the raw numbers to the logarithmic plot,
| Cost of one modular exponentiation operation (sec): | ||||
|---|---|---|---|---|
| FFA Bitness | Ch.13 (Conventional Knuth Mod. Red.) | Ch.14 (Barrettronic Mod. Red.) | ||
| 1024 | 0.395 | 0.043 | ||
| 2048 | 2.895 | 0.276 | ||
| 4096 | 21.895 | 1.703 | ||
| 8192 | 169.394 | 10.400 | ||
It would appear that "the game was worth the candles" -- we now have (AFAIK: the first and only presently-published...) fully constant-time Barrettron. And it is one that (with reasonable effort on the reader's part) fits-in-head.
In the next chapter, 15, we will begin to assemble the necessary ingredients for the generation of cryptographic primes. Please stay tuned!
~To be continued!~



Don't they normally start asking pointed questions after the first rocket explodes during launch, rather than the 256th?
Dear DangerNorm,
The rocket is not the correct model here.
Yours,
-S
6000+ words to express what the The Hymn of Breaking Strain managed in its first verse, and even then only to software. Mr. Niquette must be sophisticated indeed.
Dear DangerNorm,
And recall how A. N. Whitehead managed to fill entire bookshelf with proof of "1 + 1 = 2". This record, AFAIK, still unbroken.
Your,
-S
A reader found a corner case bug in the given algo.
And now, the fix.